Basket options and control variates

Damien LAMBERTON and Bernard LAPEYRE

July 20, 2007

Version pdf de ce document

We consider a $d$-dimensional basket model. We assume that each of the $d$ assets has a price $S^i_t$ following a Black-Scholes model driven par a brownian motion $W^i$

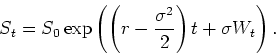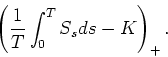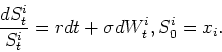
\begin{displaymath} \frac{d S^i_t}{S^i_t} = r dt + \sigma dW^i_t, S^i_0=x_i. \end{displaymath}

For the numerical examples we will consider that $d=10$ and $x_i=100$.

In order to completly specify the model we assume that

\begin{displaymath} d<W^i,W^j>_t = \rho_{ij} dt, \end{displaymath}

where $\rho_{ij}$ is a given constant matrix. Note that this matrix is necessarily a positive matrix (i.e. $\lambda . \rho \lambda \geq 0$, for every $\lambda\in\R^d$).

We will assume that $\rho_{ij}=0.5$ for $i\not=j$ and $\rho_{ii}=1$ (why ?).
  1. Prove that the variance-covariance matrix of the vector $(W^1_1,\ldots,W^d_1)$ is equal to $\rho t$. Montrer (à l'aide de SciLab) qu'elle est définie positive.
    Correction
  2. Proposer une méthode de simulation pour les vecteurs $(W^1_T,\ldots,W^d_T)$ et $(S^1_T,\ldots,S^d_T)$.
    Correction
  3. On s'intéresse maintenant au calcul du prix d'un call sur un indice de prix $I_t$ donnée par

    \begin{displaymath} I_t = a_1 S^1_t + \cdots + a_d S^d_t. \end{displaymath}

    On prendra dans les applications numériques $a_1=\cdots=a_d=1/d$. Calculer par simulation la valeur du call de payoff à l'instant $T$

    \begin{displaymath} \left(I_T-K\right)_+, \end{displaymath}

    et estimer l'erreur commise pour différentes valeurs de $K$ ($K=0.8 I_0$, $K=I_0$, $K=1.2 I_0$, $K=1.5 I_0$ par exemple).

    Reprendre les simulations pour un put sur indice de payoff $(K-S_T)_+$.

    Correction
  4. Montrez que $\E(I_T) = I_0 \exp(rT)$ et utilisez $I_T$ comme variable de contrôle. Quand cette méthode est elle efficace ?
    Correction
  5. En supposant que $r$ et $\sigma$ tendent vers $0$ se convaincre que l'on peut approximer $\log(I_t/I_0)$ par :

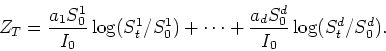
    \begin{displaymath} Z_T = \frac{a_1 S^1_0}{I_0} \log(S^1_t/S^1_0) + \cdots + \frac{a_d S^d_0}{I_0} \log(S^d_t/S^d_0). \end{displaymath}

    Montrer que $Z_T$ est un gaussienne de moyenne

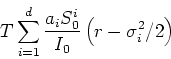
    \begin{displaymath} T \sum_{i=1}^d \frac{a_i S^i_0}{I_0} \left(r-\sigma_i^2/2\right) \end{displaymath}

    et de variance

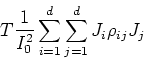
    \begin{displaymath} T \frac{1}{I_0^2} \sum_{i=1}^d \sum_{j=1}^d J_i \rho_{ij} J_j \end{displaymath}

    où $J_{i}= a_i S^i_0 \sigma_i$.

    On rappelle que (exercice) :

    \begin{displaymath} \E\left(\left(e^Z - K\right)_+\right) = e^{\E(Z)+\frac{1}{2}\Var(Z)}N(d + \sqrt{\Var(Z)}) - KN(d) \end{displaymath}

    où $d=\frac{\E(Z)-\log(K)}{\sqrt{\Var(Z)}}$.

    En déduire une expression explicite de 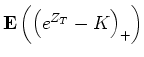$\E\left(\left(e^{Z_T} - K\right)_+\right)$ et une technique de variable de contrôle pour le calcul du prix du call. Évaluez par simulation le gain de la méthode pour différentes valeurs de $K$.

    Correction

Modèle de Paniers et fonctions d'importance

On revient un moment au modèle de Black et Scholes unidimensionnel :

\begin{displaymath} S_t = S_0 \exp\left(\left(r-\frac{\sigma^2}{2}\right)t + \sigma W_t\right). \end{displaymath}

On suppose que $S_0=100$, $\sigma=0.3$ (volatilité annuelle) et $r=0.05$ (taux d'intérêt exponentiel annuel).

  1. On se place dans la cas d'un call de strike $K$ grand devant $S_0$. Montrez par simulation que la précision relative du calcul au fur et à mesure que $K/S_0$ décroit. On prendra $S_0=100$ et $K=100$, $150$, $200$, $250$. Que se passe t'il pour $K=400$ ?
    Correction

  2. Montrer en utilisant le théorème de Girsanov que :

    \begin{displaymath} \E\left(f(W_T)\right) = \E\left(e^{-\lambda W_T -\frac{\lambda^2 T}{2}}f(W_T+\lambda T)\right). \end{displaymath}

    On se place dans le cas du call avec $S_0=100$ et $K=150$. Proposer une valeur de $\lambda$ permettant de réduire la variance de la simulation.
    Correction
  3. En utilisant le théorème de Girsanov pour les $d$ mouvements browniens proposer une technique de réduction de variance basé sur les mêmes idées dans le cas où $I_0$ est petit devant $K$.

Option sur moyenne

On s'intéresse à l'option sur moyenne de payoff donné par :

\begin{displaymath} \left(\frac{1}{T}\int_0^T S_s ds - K\right)_+ . \end{displaymath}

  1. Proposer une (ou plusieurs) méthode de discrétisation de $\int_0^T S_s ds$.
  2. En s'inspirant de la partie précedente proposer une variable de contrôle pour cette option (approximer la moyenne de l'exponentielle par l'exponentielle de la moyenne).
  3. Ecrire le théorème de Girsanov pour $W_t+\lambda t$. Expliquer comment l'utiliser lorsque $S_0$ est très petit devant $K$.