Definition of specific coupling functions. More...

#include "fluide.hpp"
#include "intersections.cpp"

Functions
double	volume_prisme (const Triangle_3 &T1, const Triangle_3 &T2)
	Computation of the signed volume of a prism. More...

double	volume_tetra (const Tetrahedron &Tet)
	Computation of the signed colume of a tetrahedron. More...

Point_3	tr (const Triangle_3 &Tn, const Triangle_3 &Tn1, const Point_3 &Xn)
	Barycentric transformation of point Xn. More...

Triangle_3	tr (const Triangle_3 &Tn, const Triangle_3 &Tn1, const Triangle_3 &T)
	Barycentric transformation of Triangle T. More...

Point_2	tr (const Triangle_3 &Tn1, const Point_3 &Xn)
	Transformation of a Point_3 into a Point_2. More...

Triangle_2	tr (const Triangle_3 &Tn1, const Triangle_3 &T)
	Transformation of a Triangle_3 into a Triangle_2. More...

Point_3	tr (const Triangle_3 &Tn1, const Point_2 &Xn)
	Barycentric transformation of a Point_2 into a Point_3. More...

Triangle_3	tr (const Triangle_3 &Tn1, const Triangle_2 &T)
	Barycentric transformation of a Triangle_2 into a Triangle_3. More...

void	Sous_Maillage_2d (const Triangles_2 &Tn, const Triangles_2 &Tn1, Triangles_2 &tri2)
	Construction of the 2d submesh of two meshes on a triangular 2d face of the solid. More...

void	sous_maillage_faceTn_faceTn1_2d (const Triangle_3 &Tn, const Triangles &tn, const Triangle_3 &Tn1, const Triangles &tn1, const Vector_3 &N, Triangles &T3d_n, Triangles &T3d_n1)
	Split the face into a submesh of the intersections of the solid face with the fluid grid at times t-dt and t. More...

Detailed Description

Definition of specific coupling functions.

Authors: Maria Adela Puscas and Laurent Monasse

Computation of fluid forces and torques acting on the solid, modifications of the fluid fluxes, filling of ghost cells, computation of the swept quantity.

Warning: Specific coupling procedures !

Function Documentation

void Sous_Maillage_2d	(	const Triangles_2 &	Tn,
		const Triangles_2 &	Tn1,
		Triangles_2 &	tri2
	)

Construction of the 2d submesh of two meshes on a triangular 2d face of the solid.

The goal is to split the solid face into interface triangles such that each triangle is fully enclosed in one single cell at times t-dt and t (npt necessarily the same cell).
Algorithm:

Construct the 2d bounding box for each triangle.
Loop on the bounding boxes.
Test the intersection of the bounding boxes using function CGAL::do_overlap(Bbox_2, Bbox_2). If the boxes intersect:
Test the intersection of the triangles using function CGAL::do_intersect(Triangle_2,Triangle_2). If the triangles intersect:
Compute the intersections between the two triangles using function CGAL::intersection(Triangle_2,Triangle_2).
If the intersection is a triangle, add it to the submesh. If the intersection is a polygon, triangulate it using class CGAL::Triangulation and function CGAL::insert in the class. If the intersection is a point or a segment, do nothing since the swept volume is null.
Warning
Specific coupling procedure !

Parameters

Tn Triangles_2

Tn1 Triangles_2

tri2 Triangles_2

Returns
void

void sous_maillage_faceTn_faceTn1_2d	(	const Triangle_3 &	Tn,
		const Triangles &	tn,
		const Triangle_3 &	Tn1,
		const Triangles &	tn1,
		const Vector_3 &	N,
		Triangles &	T3d_n,
		Triangles &	T3d_n1
	)

Split the face into a submesh of the intersections of the solid face with the fluid grid at times t-dt and t.

From the position of the interface at time t (Tn) and t-dt (Tn1), split the face into triangles fully contained in one single cell at times t and t-dt (not necessarily the same cell).
Algorithm:

Barycentric transformation of Tn using function tr(Triangle_3, Triangle_3, Triangle_3) and transformation of the resulting triangles into 2d triangles using function tr(Triangle_3, Triangle_3).
Transformation of tn1 into 2d triangles 2d using function tr(Triangle_3, Triangle_3).
Construction of the 2d submesh of the face using function Sous_Maillage_2d(const Triangles_2&, const Triangles_2&, Triangles_2&).
Transformation of the 2d submesh 2d into a 3d submesh of the face using function tr(Triangle_3, Triangle_2).

Warning: Specific coupling procedure !

Parameters

Tn	const Triangle_3: Interface triangle at time t-dt (Particule.triangles_prev)
tn	const vector<Triangle_3>: Triangulation of face Tn (Particule.Triangles_interface_prev)
Tn1	const Triangle_3: Interface at time t (Particule.triangles)
tn1	const vector<Triangle_3>: Triangulation of face Tn1 (Particule.Triangles_interface)
N	const Vector_3: exterior normal vector to Tn1 (Particule.normales)
T3d_n	vector of Triangle_3: Triangular submesh of face Particule.Triangles_interface_prev at time t-dt
T3d_n1	vector of Triangle_3: Triangular submesh of face Particule.Triangles_interface at time t

Returns: void

Point_3 tr	(	const Triangle_3 &	Tn,
		const Triangle_3 &	Tn1,
		const Point_3 &	Xn
	)

Barycentric transformation of point Xn.

Let Xn a point belonging to triangle Tn(A_1,B_1,C_1). The barycentric transform of Xn is the point Xn1 (belonging to triangle Tn1(A_2,B_2,C_2) ) given by:

$\begin{eqnarray*} \lambda = \frac{\Vert \vec{C_1 Xn} \wedge \vec{C_1 B_1} \Vert }{\Vert \vec{C_1 A_1} \wedge \vec{C_1 B_1} \Vert} \end{eqnarray*}$

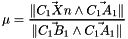
$\begin{eqnarray*} \mu = \frac{\Vert \vec{C_1 Xn} \wedge \vec{C_1 A_1} \Vert }{\Vert \vec{C_1 B_1} \wedge \vec{C_1 A_1} \Vert} \end{eqnarray*}$

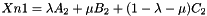
$\begin{eqnarray*} Xn1 = \lambda A_2 + \mu B_2 + (1-\lambda -\mu)C_2 \end{eqnarray*}$

Parameters

Tn	Triangle_3
Tn1	Triangle_3
Xn	Point_3

Warning: Specific coupling procedure !

Returns: Point_3

Triangle_3 tr	(	const Triangle_3 &	Tn,
		const Triangle_3 &	Tn1,
		const Triangle_3 &	T
	)

Barycentric transformation of Triangle T.

Calls function tr(Triangle_3, Triangle_3, Point_3) for each triangle vertex.

Parameters

Tn	Triangle_3
Tn1	Triangle_3
T	Triangle_3

Warning: Specific coupling procedure !

Returns: Triangle_3

Point_2 tr	(	const Triangle_3 &	Tn1,
		const Point_3 &	Xn
	)

Transformation of a Point_3 into a Point_2.

Let Triangle Tn1(A,B,C), the barycentric transform of Point_3 Xn (belonging to Tn1) into a Point_2 is given by:

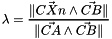
$\begin{eqnarray*} \lambda = \frac{\Vert \vec{C Xn} \wedge \vec{C B} \Vert }{\Vert \vec{C A} \wedge \vec{C B} \Vert} \end{eqnarray*}$

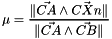
$\begin{eqnarray*} \mu = \frac{\Vert \vec{C A} \wedge \vec{C Xn} \Vert }{\Vert \vec{C A} \wedge \vec{C B} \Vert} \end{eqnarray*}$

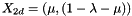
$\begin{eqnarray*} X_{2d} = (\mu, (1-\lambda-\mu)) \end{eqnarray*}$

Parameters

Tn1	Triangle_3
Xn	Point_3

Warning: Specific coupling procedure !

Returns: Point_2

Triangle_2 tr	(	const Triangle_3 &	Tn1,
		const Triangle_3 &	T
	)

Transformation of a Triangle_3 into a Triangle_2.

Calls function tr(Triangle_3, Point_3) for each triangle vertex.

Parameters

Tn1	Triangle_3
T	Triangle_3

Warning: Specific coupling procedure !

Returns: Triangle_2

Point_3 tr	(	const Triangle_3 &	Tn1,
		const Point_2 &	Xn
	)

Barycentric transformation of a Point_2 into a Point_3.

Let triangle Tn1(A,B,C), the transform of Point_2 Xn(X,Y) into a point_3 (belonging to Tn1) is given by:

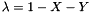
$\begin{eqnarray*} \lambda = 1- X - Y \end{eqnarray*}$

$\begin{eqnarray*} \mu = X \end{eqnarray*}$

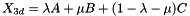
$\begin{eqnarray*} X_{3d} = \lambda A + \mu B + (1-\lambda -\mu)C \end{eqnarray*}$

Parameters

Tn1	Triangle_3
Xn	Point_2

Warning: Specific coupling procedure !

Returns: Point_3

Triangle_3 tr	(	const Triangle_3 &	Tn1,
		const Triangle_2 &	T
	)

Barycentric transformation of a Triangle_2 into a Triangle_3.

Calls function tr(Triangle_3, Point_2) for each triangle vertex.

Parameters

Tn1	Triangle_3
T	Triangle_2

Warning: Specific coupling procedure !

Returns: Triangle_3

double volume_prisme	(	const Triangle_3 &	T1,
		const Triangle_3 &	T2
	)

Computation of the signed volume of a prism.

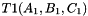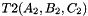The signed volume of the prism with bases the triangles $ T1(A_1,B_1,C_1) $ and $ T2(A_2,B_2,C_2) $ is given by:

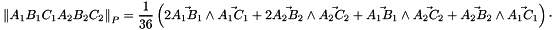
$\begin{eqnarray*} {\Vert A_1 B_1 C_1 A_2 B_2 C_2 \Vert}_P = \frac{1}{36} \left( 2 \vec{A_1 B_1} \wedge \vec{A_1 C_1} + 2 \vec{A_2 B_2} \wedge \vec{A_2 C_2} + \vec{A_1 B_1}\wedge \vec{A_2 C_2} + \vec{A_2 B_2}\wedge \vec{A_1 C_1} \right) \cdot \end{eqnarray*}$

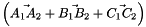
$\begin{eqnarray*} \left( \vec{A_1 A_2} + \vec{B_1 B_2} + \vec{C_1 C_2}\right)\end{eqnarray*}$

Parameters

T1	Triangle_3 basis of the prism
T2	Triangle_3 basis of prism

Warning: Specific coupling procedure !

Returns: double

double volume_tetra ( const Tetrahedron & Tet )

Computation of the signed colume of a tetrahedron.

The signed volume of a tetrahedron 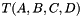$ T(A,B,C,D) $ is given by:

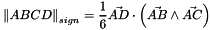
$\begin{eqnarray*} {\Vert A B C D \Vert}_{sign} = \frac{1}{6} \vec{A D} \cdot \left( \vec{A B} \wedge \vec{A C} \right) \end{eqnarray*}$

Parameters

Tet	Tetrahedron

Warning: Specific coupling procedure !

Returns: double

Functions

Detailed Description

Function Documentation