Programmation dynamique

     

Les problèmes d'optimisation dynamique ont des applications importantes aussi bien dans l'industrie qu'en gestion. Il s'agit de minimiser le coût d'une trajectoire dans un espace d'états. On dispose d'une loi d'évolution, qui détermine l'état suivant à partir de l'état courant et d'une << commande >> ; les trajectoires sont construites à partir d'un état initial et d'une suite de commandes, suivant cette loi d'évolution ; on se donne également une fonction d'objectif, définie sur les trajectoires, qu'il s'agit de minimiser. La programmation dynamique est une méthode de résolution, pour les problèmes qui satisfont au principe d'optimalité de Bellman (1955) : une sous-trajectoire d'une trajectoire optimale est elle-même optimale pour la fonction d'objectif restreinte aux trajectoires ayant pour origine celle de cette sous-trajectoire. Ce principe permet une méthode de résolution ascendante, qui détermine une solution optimale d'un problème à partir des solutions de tous les sous-problèmes.

Un exemple simple, mais classique, est celui du calcul des plus courts chemins dans un graphe, par l'algorithme de Floyd (1962) ; on doit plutôt parler de chemins à moindre coût, ce problème n'ayant aucune signification métrique.

     

Représentons un graphe à N sommets comme un tableau c d'entiers positifs de taille ; l'élément est le coût de l'arc ; si l'arc n'existe pas, on pose , de sorte qu'on travaille avec un graphe complet. Le coût d'un chemin est la somme des coûts des arcs de ce chemin. Considérons un chemin de coût minimal entre i et j et un sommet intermédiaire sur ce chemin : les sous-chemins de ce chemin, de i à k et de k à j sont aussi de coût minimal (sinon, en remplaçant un de ces sous-chemins par un chemin de moindre coût de mêmes extrémités, on diminuerait le coût du chemin de i à j, ce qui est impossible). Ce problème satisfait donc au principe d'optimalité.

  
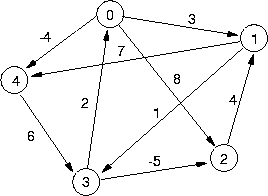
Figure: Un graphe valué par les coûts des arcs

L'algorithme de Floyd est une méthode ascendante, qui calcule successivement, pour tous les couples de sommets i, j, les chemins minimaux de i à j parmi ceux ne contenant aucun sommet intermédiaire, puis parmi ceux contenant 1, puis ceux contenant 1 et 2, etc. Notons le coût d'un chemin de i à j minimal parmi les k-chemins, c'est-à-dire ceux ayant comme sommets intermédiaires . On doit calculer à partir de . Considérons un k-chemin de coût minimum. S'il ne contient pas k, c'est un (k-1)-chemin de coût minimum ; s'il contient k, on peut le diviser en deux sous-chemins de i à k et de k à j, et par le principe d'optimalité, chacun de ces sous-chemins est un (k-1)-chemin de coût minimal ; comme l'un des deux cas se produit, on a la relation :

Voici sur l'exemple de la figure , les matrices successives, calculées d'après cette relation (on a utilisé au lieu de pour indiquer la non-existence d'un arc):

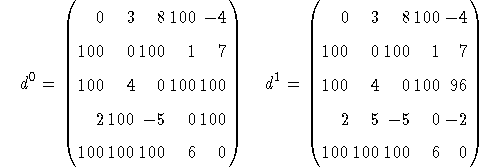
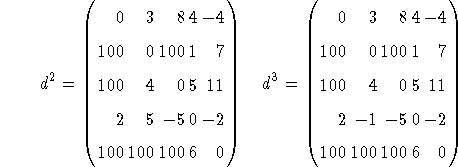
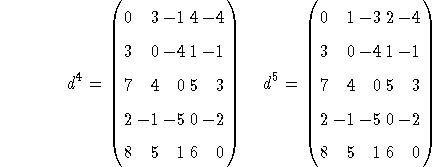
On peut interpréter cette formule récurrente comme une fonction récursive en i,j,k ; une exécution récursive conduirait à des invocations multiples, comme dans le cas de la définition récursive de la suite de Fibonacci. L'algorithme de Floyd procède au contraire par une évaluation ascendante. Pour le programmer, on a utilisé la représentation unidimensionnelle des matrices. On l'appliquera par exemple à c pour calculer les coûts minimaux dans d:

   

#define M 100
#define N 5

int c[] = {
  0, 3,  8, M, -4,
  M, 0,  M, 1,  7,
  M, 4,  0, M,  M,
  2, M, -5, 0,  M,
  M, M,  M, 6,  0
};

int d[N*N];

La fonction floyd implémente cet algorithme :

void floyd(int n, int c[], int d[]) {
  int i, j, k;
  for (i=0; i<n; i++) {
    for (j=0; j<n; j++) {
      d[i*n+j] = c[i*n+j];
      }
  }
  for (k=0; k<n; k++) {
    for (i=0; i<n; i++) {
      for (j=0; j<n; j++) {
        int u = d[i*n+k] + d[k*n+j];
        if (u < d[i*n+j]) {
          d[i*n+j] = u;
        }
      }
    }
  }
}

Il est facile de modifier cet algorithme pour être capable de construire les chemins minimaux : il suffit de conserver dans un autre tableau le k optimal.