1.6 Définitions récursives

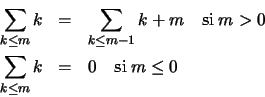
Une définition de fonction est récursive si son corps contient une expression d'invocation d'elle-même, dite invocation récursive . L'intérêt des définitions récursives est double. D'une part, elles permettent de transcrire de façon quasiment littérale certaines définitions mathématiques, souvent appelées récurrentes. Ainsi la transcription de l'identité

$$\begin{eqnarray*} \sum_{k\le m} k &= &\sum_{k\le m-1} k + m \quad\mbox{si } m>0 \\ \sum_{k\le m} k &= &0\quad\mbox{si } m\le 0 \end{eqnarray*}$$

donne immédiatement la définition récursive suivante :

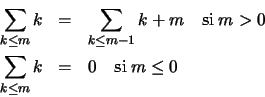
package exemples;

class Récursion {
  static int sommerEntiers(int m) {
    return (m <= 0) ? 0 : sommerEntiers(m-1) + m;
                       // invocation récursive
  }
  public static void main(String[] args) {
    System.out.println("somme de 1 à 3 = " + sommerEntiers(3));  
                       // --> 6
  }
}

Une définition récursive comporte toujours une condition d'arrêt, qui est ici m <= 0.

Le mécanisme d'invocation des fonctions s'applique en particulier aux fonctions définies récursivement. Par exemple, une invocation sommerEntiers(3) dans le corps de main provoque la suite d'invocations :

$$\verb*\vert main(...)\vert \to \verb*\vert s(3)\vert \to \ve... ... s(2)\vert \to \verb*\vert s(1)\vert \to \verb*\vert s(0)\vert$$

et la suite de retours, qui retourne finalement 6 à main(...) :

$$\verb*\vert s(0)\vert \stackrel{0}{\to} \verb*\vert s(1)\ve... ...b*\vert s(3)\vert \stackrel{6}{\to} \verb*\vert main(...)\vert$$

L'évolution de la pile pendant cette invocation est la suivante :

$$\begin{eqnarray*} \begin{array}[b]{c} \vert s(3) \end{array}\to \begin{array}[b]... ...rt s(3) \end{array}\to \begin{array}[b]{c} \vert s(3) \end{array}\end{eqnarray*}$$

1.6.0.0.1 Les fonctions des informaticiens

Les mathématiciens définissent maintenant les fonctions comme des relations, c'est-à-dire des sous-ensembles du produit cartésien de deux ensembles qui vérifient simplement des propriétés d'existence et d'unicité (tout élément a une image et une seule) : c'est ainsi que les fonctions sont comprises en théorie des ensembles. Les informaticiens n'adoptent pas cette définition. Pour eux, une fonction n'est pas seulement un ensemble de couples, mais est une méthode de calcul (ou algorithme). Ainsi, la fonction sommerEntiers définie auparavant à partir de l'expression $m(m+1)/2$ et celle définie-ci récursivement, bien que déterminant le même ensemble de couples (on dit qu'elles sont égales en extension), ne sont pas identiques d'un point de vue calculatoire : l'une réalise une addition, une multiplication et une division, l'autre réalise $m$ soustractions et $m$ additions.

Un exemple classique de définition récursive est celui de la fonction factorielle, pour laquelle il n'existe pas d'expression arithmétique :

package exemples;

class Récursion {
  static int fact(int n) {
    return (n == 0) ? 1 : n*fact(n-1);
                         // fact(n-1) est une invocation récursive
    }
  }
  public static void main(String[] args) {
    System.out.println("fact(3) = " + fact(3));        // --> 6
  }
}

1.6.0.0.2 Diviser pour régner

D'autre part, on obtient facilement des définitions récursives à partir de la conception récursive d'un algorithme : pour résoudre un problème par un algorithme, on applique ce même algorithme à un ou plusieurs sous-problèmes. Cette méthode, appelée diviser pour régner permet d'écrire assez facilement des algorithmes parmi les plus intéressants, voire les plus efficaces.

Figure: Recherche d'un zéro par dichotomie

La dichotomie est un exemple simple de cette méthode. On cherche à calculer un zéro d'une fonction réelle continue $f$ sur un intervalle $[a,b]$, prenant des valeurs de signes opposés aux extrémités. Le théorème des valeurs intermédiaires assure l'existence d'un zéro. L'idée de la dichotomie est de chercher un zéro sur $[a,(a+b)/2]$ ou bien sur $[(a+b)/2,b]$, selon le signe de $f((a+b)/2)$.

package exemples;

class Dichotomie {
  static double f(double x) { ... }

  static final double EPS = 1e-5;

  static double zéro(double a, double b) 
    // on suppose que f(a)*f(b) < 0
  {
    double m = (a+b)/2;
    double fm = f(m);
  
    if (Math.abs(fm)<EPS) {
      return m;
    } else {
      if (f(a)*fm<0) {
        return zéro(a,m);
      } else {
        return zéro(m,b);
      }
    }
  }
}

La condition d'arrêt est Math.abs(fm)<EPS, EPS étant une variable de la classe Dichotomie, et Math.abs étant la fonction qui calcule la valeur absolue d'un double.

La portée d'une variable d'une classe comprend cette classe.

1.6.0.0.3 Récursivité multiple

Quand le corps d'une fonction comporte plusieurs invocations récursives, leur évaluation est organisée sous la forme d'un arbre. L'exemple classique est celui de la définition récursive de la suite de Fibonacci :

  static int fib(int n) {
    return n<=1 ? 1 : fib(n-1) + fib(n-2);
  }

La figure  représente l'arbre des invocations de fib(4), et la figure  représente les états successifs de la pile, pour une invocation de fib(4) dans main(...) (pour alléger, les cadres d'invocation de main(), fib(4), fib(3), etc, y sont désignés par m, 4, 3, etc). On remarquera que certaines invocations sont exécutées plusieurs fois : fib(2) est exécutée deux fois, fib(1) trois fois, fib(0) deux fois. Rappelons que les sous-expressions étant évaluées de gauche à droite, l'invocation fib(n-1) est évaluée avant fib(n-2).

Figure: Arbre d'invocation de la suite de Fibonacci

Figure: Évolution de la pile pour la suite de Fibonacci

1.6.0.0.4 Récursivité mutuelle

Un ensemble de définitions de fonctions est mutuellement récursif si la relation « $f$ invoque $g$ » admet un cycle : $f_1$ invoque ...invoque $f_n$ invoque $f_1$. L'exemple suivant est classique (et sans grand intérêt) :

class Parité {
  static boolean impair(int n) {
    if (n == 0) {
      return false;
    } else {
      return pair(n-1);
    }
  }
  
  static boolean pair(int n) {
    if (n == 0) {
      return true;
    } else {
      return impair(n-1);
    }
  }
}

Les fonctions Parité.pair et Parité.impair s'invoquent mutuellement :

$$\mathtt{pair}(3) \to \mathtt{impair}(2) \to \mathtt{pair}(1) \to \mathtt{impair}(0)$$

La dernière invocation retourne false :

$$\ \mathtt{impair}(0) \stackrel{\mathtt{false}}{\to} \mathtt{... ...htt{pair}(3) \stackrel{\mathtt{false}}{\to} \texttt{main(...)}$$

Les définitions mutuellement récursives sont surtout utiles pour travailler sur des structures de données mutuellement récursives, par exemple en analyse syntaxique.