Pour ces travaux pratiques d'introduction à Scilab, il vous faut lancer le logiciel Scilab et disposer ainsi d'une fenêtre permettant de saisir et d'exécuter des instructions.
Dans ces premiers travaux pratiques, vous trouverez une série de lignes de commandes Scilab précédées du signe -->. Pour commencer, il vous suffit de les recopier ou de les saisir par copier-coller (sans -->) pour les exécuter immédiatement dans la fenêtre Scilab.
Pour des successions de lignes de commandes, il est préférable de disposer d'un éditeur (Emacs), d'ouvrir un fichier (par exemple nom_du_fichier.sce), d'y écrire les lignes de commandes puis de les exécuter en tapant sous Scilab l'instruction :
On peut également utiliser la rubrique File Operations du menu File.
Toute ligne débutant par // est une ligne de commentaires.
Pour effectuer des graphiques en deux dimensions, on utilise la commande plot2d.
Dans le menu de la fenêtre graphique, sélectionner File, puis Export pour exporter le graphique (au format Postscript par exemple, ou au format Postscript-Latex qui permet une insertion facile dans un fichier LATEX).
La fonction Scilab plot2d a de nombreux arguments optionnels permettant de spécifier des attributs d'un graphique : couleur, style et épaisseur des traits, échelle, dimensions du cadre, etc. Pour découvrir ces arguments optionnels, taper help plot2d.
Pour découvrir les attributs associés aux objets graphiques, utiliser le menu Edit de la fenêtre graphique. À travers ce menu, on peut également modifier en temps réel des attributs.
À titre indicatif, noter que les manipulations des attributs d'un graphique peuvent également être effectuées au moyen de commandes Scilab (taper help graphics_entities).
Nous allons illustrer des manières de changer les attributs d'un graphique 2D.
L'option style permet notamment de changer la couleur.
Ce changement de couleur peut également être obtenu en utilisant le menu Edit de la fenêtre graphique.
Question 1 Essayez, à l'aide du menu Edit, de modifier la couleur et de rajouter des losanges aux points de la courbe. Pour cela, on cherchera Polyline dans le menu déroulant des entités graphiques.
L'option rect permet de fixer les échelles.
Question 2 Effectuer la même manipulation à l'aide du menu Edit.
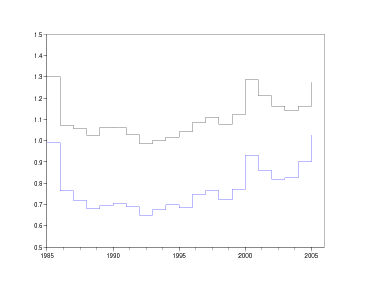
Le tableau de chiffres suivant représente l'indicateur de pouvoir d'achat du franc de 1985 à 2001, exprimé en euros 2005 (source Insee). Il permet de traduire en euros 2005 des valeurs exprimées en francs du passé. Sur une ligne, on trouve
Ainsi, 1 000 F de 1985 équivalent, en pouvoir d'achat, à 231,36 euros de 2005.
Le tableau de chiffres suivant représente l'indicateur de pouvoir d'achat de l'euro de 2002 à 2005, exprimé en euros 2005 (source Insee). Il permet de traduire en euros 2005 des valeurs exprimées en euros du passé.
Par copier-coller, transférer les deux séries de lignes précédentes dans deux fichiers francs.txt et euros.txt. On prendra garde à ce que le fichier finisse par un retour à la ligne, sinon la dernière ligne ne sera pas lue par fscanfMat. On va à présent lire les contenus de ces fichiers et stocker les résultats de la lecture dans deux matrices Mf et Me (à 2 colonnes et n lignes). Pour cela utiliser help fscanfMat :
Question 3 À partir des matrices Mf et Me, construire une matrice 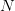 dont la première
colonne soit les années de 2005 à 1985, et la deuxième l'indicateur de pouvoir d'achat de
l'euro exprimé en euros 2005. On rappele que 1 EUR= 6,55957 FF.
dont la première
colonne soit les années de 2005 à 1985, et la deuxième l'indicateur de pouvoir d'achat de
l'euro exprimé en euros 2005. On rappele que 1 EUR= 6,55957 FF.
En utilisant M=N($:(-1):1,:), transformer cette matrice en une dont la première colonne soit les années de 1985 à 2005.
Question 4 Le tableau précédent représente, en euros courants, les prix des carburants (source direction générale de l'énergie et des matières premières, ministère de l'Industrie) en hectolitres. On touve sur une ligne : année, supercarburant, gazole.
Par copier-coller, transférer la série de lignes précédente dans un fichiers carburants.txt. Saisir le tableau dans une matrice Cc. Convertir ces prix, exprimés en euros courants,en euros de 2005 et les ramener de l'hectolitre au litre. Tracer sur un même graphique les évolutions des prix (en euros de 2005) des deux carburants de 1985 à 2005.
Scilab est un langage interprété où la transmission des arguments se fait par valeur, même pour les objets de type matrices. Il faut donc éviter les boucles qui peuvent être très inefficaces en terme de temps de calcul. Pour cela, il faut utiliser si possible des opérateurs vectoriels qui font la même chose.
Nous recommandons ici de disposer d'un éditeur (Emacs), d'ouvrir un fichier (par exemple nom_du_fichier.sce), d'y écrire les lignes de commandes puis de les exécuter en tapant sous Scilab exec("nom_du_fichier.sce").
On peut définir une fonction Scilab de façon interactive, mais il est souvent plus naturel d'écrire le code d'une fonction dans un fichier au moyen d'un éditeur de texte.
On peut mélanger des instructions Scilab et des définitions de fonctions dans un même fichier, qu'on fera terminer par l'extension .sce.
L'entête d'une fonction est constituée de la séquence
function [<arguments de retour>]=<nom>(<arguments d'entrée>)
et le corps de la fonction est terminé par le mot clef endfunction.
On notera l'utilisation de l'opérateur .^ (et non pas simplement ^) car l'argument  est
généralement un vecteur (et non pas un scalaire).
est
généralement un vecteur (et non pas un scalaire).
Voici un autre exemple de fonction.
Question 5 Écrire la fonction sinus cardinal (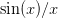 ) de telle sorte qu'elle puisse
admettre un argument
) de telle sorte qu'elle puisse
admettre un argument  vectoriel et retourne un vecteur de même taille contenant le sinus
cardinal de chacun de ses éléments. Deux problèmes se posent : comment faire une division
vectorielle ? comment éviter une divison par zéro ?1
vectoriel et retourne un vecteur de même taille contenant le sinus
cardinal de chacun de ses éléments. Deux problèmes se posent : comment faire une division
vectorielle ? comment éviter une divison par zéro ?1
Une fonction dans Scilab peut avoir plusieurs arguments, scalaires ou vectoriels.
Une fonction dans Scilab peut renvoyer plusieurs valeurs.
Si on tape simplement
seule la première valeur est retournée. Pour disposer de toutes les valeurs, il faut utiliser la syntaxe suivante qui attribue des noms à ces valeurs
Les deux fonctions ci-dessous retournent une permutation de 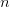 éléments tirée au hasard.
Interpréter le mécanisme de simulation de la première des deux. Il apparaît que cette
méthode est plus lente que l'appel à la fonction Scilab grand.
éléments tirée au hasard.
Interpréter le mécanisme de simulation de la première des deux. Il apparaît que cette
méthode est plus lente que l'appel à la fonction Scilab grand.
On considère un emprunt
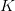 , capital emprunté ;
, capital emprunté ;
![θ ∈ [0,1]](intro_scilab_227x.png) ;
;
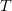 périodes (
périodes (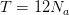 pour un remboursement mensuel sur
pour un remboursement mensuel sur 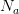 années) ;
années) ;et on veut connaître
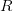 du remboursement par période ;
du remboursement par période ;
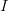 des intérêts ;
des intérêts ;
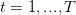
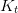 le capital restant dû ;
le capital restant dû ;
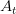 le capital amorti ;
le capital amorti ;
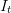 les intérêts dus.
les intérêts dus. Le taux actuariel  est (dans le cas de remboursements mensuels)
est (dans le cas de remboursements mensuels)
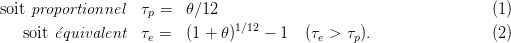
On a les relations suivantes ( ) :
) :

 , capital emprunté, on en déduit pour
, capital emprunté, on en déduit pour  :
: 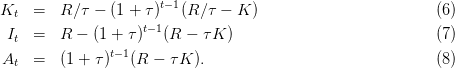
Introduisons la fonction suivante (telle que 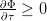 ) :
) :
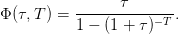 | (9) |
Avec 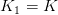 et
et 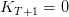 (plus de capital restant dû après la dernière échéance), on
obtient alors facilement :
(plus de capital restant dû après la dernière échéance), on
obtient alors facilement :
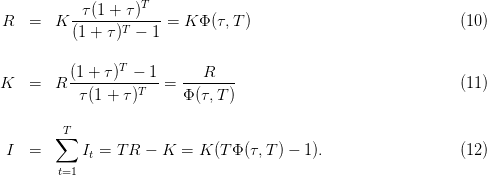
Question 6 Copier le code Scilab ci-dessus dans un fichier calculs_emprunt.sce et charger la fonction emprunt par la commande exec("calculs_emprunt.sce"). Choisir des paramètres d'emprunt, puis étudier l'effet d'une variation de 1 % du taux annuel. Modifier le code précédent pour qu'il fournisse également en sortie le montant total des intérêts.
Question 7 Programmer une fonction capital_emprunt de la forme [capital]=capital_emprunt(mensualite,taux_annuel,annees), donnant le capital pouvant être emprunté en fonction de la mensualité, du taux et du nombre d'années.
Si l'on veut calculer, pour un plan d'épargne logement (pel), le capital que l'on peut emprunter et les mensualités, il faut procéder comme suit. Un pel terminé se caractérise par
 (intérêts acquis sur le pel) ;
(intérêts acquis sur le pel) ;
 du pel.
du pel. Le capital empruntable 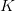 dépend du nombre
dépend du nombre 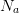 d'années d'emprunt : il est tel que les
intérêts perçus
d'années d'emprunt : il est tel que les
intérêts perçus 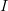 (par le prêteur pour un prêt au taux
(par le prêteur pour un prêt au taux 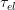 ) soient égaux à
) soient égaux à 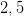 fois les
intérêts acquis (sur le pel), soit
fois les
intérêts acquis (sur le pel), soit
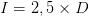 | (13) |
(2,5 doit être remplacé par 1,5 pour un livret ou compte d'épargne). On en déduit
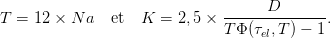 | (14) |
Enfin, le capital est plafonné à 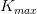 (92 000 euros en 2003) et le prêt est accordé à un
taux (actuariel)
(92 000 euros en 2003) et le prêt est accordé à un
taux (actuariel) 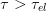 :
:
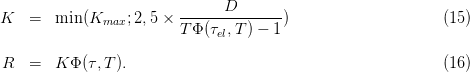
Question 8 Programmer une fonction PEL_emprunt de la forme [capital,mensualite]=PEL_emprunt(droits_a_pret,taux_annuel,annees), donnant le capital pouvant être emprunté et le montant des remboursements, en fonction des droits à prêt, du taux annuel du pel et du nombre d'années d'emprunt.
Question 9