Contents

Introduction L'organisation des sociètés animales s'apprette depuis longtemps à de nombreuses études, y compris mathématiques. C'est le cas pour la fourmi. L'un des problème souvent étudié est la gestion des cadavres, et c'est ce problème que nous étudierons. Mais posons tout d'abord le problème: il s'agit de modéliser le comportement des fourmis vivantes vis à vis cadavres de formis mortes. Des expériences réalisées avec des fourmis montrent que certaines fourmis ont tendances à regrouper les fourmis mortes en tas. Cependant ce regroupement ne se fait pas de façon aléatoire: en effet les fourmis montrent que les fourmis ont tendances à regrouper les cadavres. Il existe plusieurs manières de traiter ce problème, nous utiliserons une méthode probabiliste, cependant il existe également des méthodes déterministe.

Description de l'expérience

1 Description de l'environment

On part d'un disque contenant plusieurs tas de fourmis mortes. Nous y étudierons après l'introduction de fourmis vivantes peuvant déplacer des cadavres, l'évolution de la taille des tas: pour simplifier notre modélisation, nous placerons les tas de fourmis mortes sur le bord du disque de manière uniforme.

Le temps est pris discret; le pas de temps correspond au temps nécessaire à une fourmi pour se déplacer et choisir de prendre ou de déposer un cadavre.

2 Comportement d'une fourmi

2.1 Prise et dépôt d'un cadavre

Différentes expériences références nous montrent que globalement le comportement des fourmis pour la prise et le dépôt est le suivant:

• pour la prise, la fourmi aura d'autant plus envie de prendre un cadavre que le tas de fourmi est petit, car dans ce cas il lui est plus facile de prendre un cadavre;
• pour le dépôt, c'est la situation inverse, la fourmi aura d'autant plus envie de déposer le cadavre que le tas de fourmi est gros.

2.2 Déplacement

Dans notre modélisation, nous considérerons que la fourmi peut se déplacer tout autour du disque. Nous considérons qu'elle a une aversion à parcourir de longues distances ainsi, la probabilité qu'elle reste au même endroit où que celle qu'elle se déplace sur les tas voisins sera beaucoup plus importante qu'elle traverse le disque pour aller sur le tas diamétralement opposé. Nous considérons que la vitesse de déplacement n'est pas affectée par le poids d'un cadavre.

Modèle et algorithme

3 Schéma de l'algorithme

Dans ce chapitre, nous allons décrire la structure générale de l'algorithme.
On considère deux matrices

• La première est un vecteur de “la taille du nombre de tas” N et associe à chaque coordonnée la taille du tas de fourmis mortes associée. Dans chaque boucle, on notera Tasold la matrice que l'on vient de calculer, et Tasnew celle que l'on est en train de calculer.
  
• La deuxième est une matrice définissant l'état des fourmis vivantes. Sa taille est (M, 2), chaque ligne représente une fourmi, la première colonne va définir la configuration de la fourmi: Si elle est seule on aura 1, si elle est chargée d'un cadavre, on aura 2; la deuxième colonne définira l'emplacement des fourmis. On utilisera le même principe de notation que pour la matrice des tas:on notera fold la matrice que l'on a calculer, et fnew celle que l'on calcule.
  

Le programme va contenir deux grandes boucles:

• la première est la boucle en temps,
• la seconde concerne le nombre des fourmis vivantes.
  

Par soucis de clarté, nous ferons apparaître 3 macros: pour la prise, le dépôt, et le déplacement. A chaque pas de temps, chaque fourmi pourra se déplacer et prendre ou déposer un cadavre suivant son état.
La structure générale du programme est la suivante:

Le programme se fini par une réinitialisation des matrice de tas et d'état des fourmis vivantes. Les sous-parties du programme sont expliquées à la suite.

4 Conditions initiales

Dans cette sous section nous allons définir les conditions initiales qui serviront dans tout l'algorithme.

1. Nombre de pas de temps M.
   
2. Conditions initiales sur les fourmis vivantes. On va tout d'abord définir le nombre de fourmis vivantes qui serviront à déplacer les cadavres Fou, puis nous définirons l'emplacement initial des fourmis vivantes avec le fichier placeini∗.sce.Il peut être définit de plusieurs manières:
   • On peut les disposer tous au même tas (placeini1.sce):
     function[F]=placeini1(Fou,N)  
     F=N*ones(Fou,1);  
     

   • On peut décider de les répartir aléatoirement sur le cercle (placeini2.sce):
     function[F]=placeini2(Fou,N)  
     F=ones(Fou,1)+(N-1)*rand(Fou,1);  
     

   • On peut encore choisir de les répartir manuellement en définissant dans les données initiales du programme la colonne fold(1 : Fou, 2).
     

   Pour pouvoir choisir la condition initiale que l'on veut, il suffit d'aller au début du programme et de choisir le numéro correspondant aux conditions que l'on souhaite:

   placeini=placeini*.  
   

3. et les conditions initiales sur le nombre et la répartition des fourmis mortes:

Dans un premier temps, nous définirons le nombre de tas de fourmis que l'on prend à l'origine N. Puis, dans un deuxième temps, il faudra définir la répartition des fourmis mortes à l'instant initial. Cette fonction ne dépendra que de N, le nombre de tas de fourmis mortes, on appelle tasini ∗ .sce ce fichier.
On aura donc plusieurs manières de définir cette fonction:

• On peut choisir une répartition uniforme (tasini1.sce):
  function[F]=tasini1(N)  
  for i=1:N  
  F(i)=10;  
  end  
  

• On peut choisir une répartition aléatoire (tasini2.sce):
  function[F]=tasini2(N)  
  F=10*rand(10,1);  
  

• On peut choisir de ne modifier qu'un seul tas (tasini3.sce):
  function[F]=tasini3(N)  
  F(1)=25;  
  for i=2:N  
  F(i)=10;  
  end  
  

• On peut choisir de prendre une répartition croissante (tasini4.sce):
  function[F]=tasini4(N)  
  for i=1:N  
  F(i)=2*i;  
  end  
  

Dans tout les cas il sera très utile de connaître la somme totale des fourmis mortes Tt présentes sur le disque. Pour cela nous utiliserons la commande sum:

Pour pouvoir choisir la condition initiale que l'on veut, il suffit d'aller au début du programme et de choisir le numéro correspondant aux conditions que l'on souhaite:

Il est très intéressant de faire varier ces conditions initiales, car elles influencent beaucoup les résultats des tests que nous feront. La liste proposée ici vous donne quelques exemples de répartions, mais si vous avez d'autres idée n'hésitez pas!

5 Modèle de prise

5.0.1 Prise d'un cadavre

La macro Prise qui est chargé de gérer la prise des fourmis. La fourmi est au temps n− 1 seule, et a la possibilité au temps n de prendre ou pas une fourmi au tas où elle se trouve. Pour que la fourmi puisse prendre un cadavre, il faut vérifier que le tas n'est pas vide! Cette dernière remarque est très importante, il faut donc au préalable faire un test pour savoir si le tas n'est pas vide. Dans ce cas, on force la matrice des tas à rester identique, et la fourmi a être seule. Considérons maintenant que le tas où se situe la fourmi n'est pas vide. La fourmi a la possibilité de prendre ou pas une fourmi de ce tas. La loi de prise sera une loi binomiale de paramètre p. Cette loi est contenue dans le programme prisedepot; nous étudierons ce programme plus tard. Enfin, ce programme se termine par la fonction de comptage. Celle-ci ve servir à redéfinir l'état de la matrice de “l'état des fourmis vivantes” en fonction du choix que la fourmi a fait de prendre ou pas le cadavre.

5.0.2 le programme de prisedepot

Ce programme simule la loi de prise/dépôt selon une loi de bernoulli 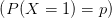de paramètre p. Avec pour expression de p:

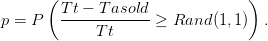(1)

Le programme :

6 Modèle de décharge

6.0.1 Dépôt d'un cadavre

Elle se situera dans la macro Depot. La structure de ce programme est calquée sur le programme Prise.
On considére une fourmi chargée à l'instant n− 1. Elle a la possibilité de se déplacer puis de déposer son cadavre sur un autre tas à l'instant n. La principale différence entre cette partie et la précédente réside dans le fait qu'il n'y a pas de condition au préalable sur le tas à avoir pour que la fourmi puisse déposer un cadavre.
Nous allons nous placer à l'instant n après le déplacement de la fourmi. La probabilité pour que la fourmi dépose le cadavre qu'elle transportait dépend de la taille du tas: la fourmi aura d'autant plus envie de déposer son cadavre sur un tas que celui-ci sera grand, ce qui est l'inverse que pour le modèle de prise. La partie de sous programme s'écrira. La fonction de comptage fonctionne de la même manière que celle du programme Prise.

7 Modèle de déplacement

7.1 Présentation

On modélise ici le déplacement d'une fourmi et son aversion à parcourir de grandes distances. Ceci est présenté dans le programme deplace Comme on peut le voir sur le schéma 2, à chaque déplacement, la fourmi peut rejoindre n'importe quelle autre position sur le cercle.

g

Le principe de ce programme est le suivant: il faut simuler une loi sur (1,...,n). On va, dans un premier temps, calculer l'inverse de la distance à l'origine (l'origine, ici, étant le point où se trouve la fourmi à l'instant n − 1) en chacun des points du disque (voir schéma 3). Puis on va créer un segment qui aura pour taille la somme de ces inverses. On tirera alors une variable aléatoire dans ce segment, et on associera à ca valeur le points correspondant sur le cercle. Pour tenir compte du fait que la fourmi peut rester au même endroit, on ajoute à ce segment un deuxième segment dont la taille fait la moitié du précédent. Si la variable aléatoire tombe dans cette partie du segment, la fourmi restera au même endroit. On peut noter qu'à chaque période la fourmi a deux fois plus de chance de déplacer que de rester au même endroit.

Le calcul de la distance de chaque tas à l'origine se fera par le calcul du module du vecteur correspondant. L'algorithme sera donc:

7.2 Perspectives

On peut apporter de nombreuses modification dans le but d'affiner la modélisation:

• on peut par exemple tenir compte de la fatigue des fourmis: plus le temps avance et moins la fourmi aura envie d'effectuer des long trajet;
  
• on peut également tenir compte de la fatigue dûe au transport d'un cadavre: si la fourmi en transporte une autre elle aura encore plus d'aversion à effectuer des longs trajets;
  
• la fourmi peut encore être attirée par des tas où il y a moins de fourmis vivantes;
  
• on peut encore modifier la modélisation proposée pour l'attente, etc...
  

Représentation des résultats

8 Visualisation

La représentation des résultats devra rendre compte de l'évolution de tous les tas de fourmis mortes dans le temps. C'est la raison pour laquelle nous utiliserons une représentation en histogramme 3D, ceci avec la commande hist3D de Scilab. La représentation en cylindre étant impossible, nous ferons une réprésentation linéique avec la correspondance suivante:

La représentation des résultats soulève un autre problème, celui du nombre de pas de temps à représenter: on ne peut pas afficher l'évolution de chaque pas de temps sur les graphiques, car ceux-ci deviennent alors illisibles. On crée alors une fréquence d'échantillonage e qui nous permettra de n'afficher qu'une sous-partie des mesures à chaque pas de temps. On pourra modifier cette fréquence en début de programme.

9 Mise en œuvre informatique

La commande hist3D a pour argument: hist3D(F,teta,alpha), où F est une matrice, et teta et alpha deux angles de vision du graphique. Ces deux angles seront fixés une fois pour toutes, de manière à obtenir un graphique le plus lisible possible. Reste donc à créer une matrice F qui pourra rendre compte de l'évolution des tas à chaque période.
C'est la raison pour laquelle on insère dans la boucle en temps une une matrice qui va conserver la valeur des tas à chaque pas de temps:

Voici la commande:

A partir de cette matrice on va créer une seconde matrice qui va tenir compte de la fréquence d'échantillonage e de cette matrice qui nous servira à la représentation graphique:

Travaux pratiques

10 utilisation du code

Nous partons d'une répartion uniforme en fourmis mortes, et d'une répartition aléatoire des fourmis vivantes. On va procéder à trois essais avec M = 500 unité de pas de temps, N = 10 tas de fourmis mortes et 100 fourmis mortes au total, Fou = 10 fourmis vivantes. On fixe la fréquence d'échantillonnage à e = 4. Nous obtenons par exemple les trois courbes suivantes:

11 Étude d'un cas

Nous partons d'une répartition uniforme en fourmis mortes, et d'une répartition aléatoire des fourmis vivantes et nous étudirons la convergence du système en fonction du nombre initiale de fourmis mortes, ainsi que du nombre de fourmis vivantes. On va procéder à trois essais avec M = 500 unité de pas de temps, N = 10 tas de fourmis mortes, on fixe la fréquence d'échantillonnage à e = 4.

On prend Fou = 10 fourmis vivantes.

On prend Tt = 100 fourmis mortes.

12 Modification du code

Cette partie propose de modifier une partie du code. Plus précisement il s'agit de modifier une des macros du programme: on peut ainsi modifier les macros de prise et de dépôt, ou bien modifier la macro de déplacement, c'est à dire modifier la loi que l'on a simulé.

12.1 Modification de la macro de déplacement

Dans un deuxième temps, nous vous proposons de modifier cette macro de la manière suivante: nous allons non seulement tenir compte de l'aversion à parcourir les longues distances, mais aussi de la fatigue des fourmis: plus le temps va augmenter, et moins la fourmi aura tendance à parcourir de longs trajets.

12.2 Modification des macros de prise et de dépôt

Les macros de prise et de dépôt simulent une loi de Bernoulli. Cependant le paramètre de cette loi a été choisit de manière arbitraire.