CELIA3D  1.0
Fluid-structure interaction using cut-cells
Public Member Functions | Data Fields
Grille Class Reference

Definition of class Grille. More...

#include <fluide.hpp>

Public Member Functions

 Grille ()
 Default constructor. More...
 
 Grille (int Nx0, int Ny0, int Nz0, double dx0, double x0, double dy0, double y0, double dz0, double z0)
 Overload of the constructor. More...
 
 ~Grille ()
 Destructor. More...
 
void affiche ()
 Test display. More...
 
void affiche (string r)
 Test display. More...
 
Cellule cellule (int i, int j, int k)
 Access cell (i,j, k). More...
 
Cellule in_cell (const Point_3 &p)
 Access the cell containing point p. More...
 
void in_cell (const Point_3 &p, int &i, int &j, int &k, bool &interieur)
 Access cell containing point p. More...
 
void Init ()
 Definition of initial conditions. More...
 
double pas_temps (double t, double T)
 Computation of the fluid time-step. More...
 
void BC ()
 Boundary conditions. More...
 
double Masse ()
 Computation of the total fluid mass. More...
 
double Impulsionx ()
 Computation of the total fluid x-momentum. More...
 
double Impulsiony ()
 Computation of the total fluid y-momentum. More...
 
double Impulsionz ()
 Computation of the total fluid z-momentum. More...
 
double Energie ()
 Computation of the total fluid energy. More...
 
void Impression (int n)
 Print out results. More...
 
void solve_fluidx (const double dt)
 Solve the fluid equations in the x direction. More...
 
void solve_fluidy (const double dt)
 Resolution of fluid equations in the y direction. More...
 
void solve_fluidz (const double dt)
 Resolution of the fluid equations in the z direction. More...
 
void melange (const double dt)
 Mixing the cells with negative density or pressure with neighbours. More...
 
void fnumx (const double sigma, double t)
 Computation of the numerical x-flux. More...
 
void fnumy (const double sigma, double t)
 Computation of the numerical y-flux. More...
 
void fnumz (const double sigma, double t)
 Computation of the numerical z-flux. More...
 
void corentx (double sigma)
 Entropy correction in the x direction. More...
 
void corenty (double sigma)
 Entropy correction in the y direction. More...
 
void corentz (double sigma)
 Entropy correction in the z direction. More...
 
void Solve (const double dt, double t, int n, Solide &S)
 Resolution of the fluid equations. More...
 
void Forces_fluide (Solide &S, const double dt)
 Computation of fluid forces (Particule.Ff) and torques (Particule.Mf) applied on the Solide. More...
 
void Modif_fnum (const double dt)
 Modification of fluid fluxes and discrete balance on a cell (cut-cell method). More...
 
void Mixage ()
 Conservative mixing of small cut-cells. More...
 
void Fill_cel (Solide &S)
 Filling of the ghost cells (alpha = 1) More...
 
void swap_face (const Triangles &T3d_prev, const Triangles &T3d_n, const double dt, Particule &P, double &volume_test)
 Computation of the quantity of fluid swept by an interface triangle between t-dt and t, and computation of the boundary flux. More...
 
void swap_face_inexact (const Triangle_3 &Tr_prev, const Triangle_3 &Tr, const Triangles &T3d_prev, const Triangles &T3d_n, const double dt, Particule &P, double &volume_test)
 Computation of the swept quantity for an interface triangle between times t-dt and t. Computation of the boundary flux. More...
 
void cells_intersection_face (int &in, int &jn, int &kn, int &in1, int &jn1, int &kn1, std::vector< Bbox > &box_cells, std::vector< Cellule > &Cells)
 List of fluid cells intersected by an interface triangle between times t-dt and t. More...
 
void Swap_2d (const double dt, Solide &S)
 Computation of the quantity of fluid swept by the solid between times t-dt and t. More...
 
void Swap_3d (const double dt, Solide &S)
 
Cellule voisin_fluide (const Cellule &c, bool &target)
 
Cellule voisin_mixt (const Cellule &c, bool &target)
 
Cellule voisin (const Cellule &c)
 
Cellule cible (const Cellule &c, std::vector< std::vector< int > > &tab_cible)
 
void Mixage_cible ()
 Conservative mixing of small cut-cells. More...
 
bool Mixage_cible2 ()
 Conservative mixing of small cut-cells. More...
 
void Parois_particles (Solide &S, double dt)
 Intersection of the fluid grid with solid. More...
 
std::vector< Point_3 > intersection (Triangle_3 t1, Triangle_3 t2)
 

Data Fields

double x
 Position of the origin of the fluid grid. More...
 
double y
 
double z
 
double dx
 Spatial discretization step. More...
 
double dy
 
double dz
 
vector< vector< vector< Cellule > > > grille
 Fluid mesh. More...
 

Detailed Description

Definition of class Grille.

Constructor & Destructor Documentation

Grille::Grille ( )

Default constructor.

Variable grille represents the fluid mesh, it is a 3D array of Cellule.

Grille::Grille ( int  Nx0,
int  Ny0,
int  Nz0,
double  dx0,
double  x0,
double  dy0,
double  y0,
double  dz0,
double  z0 
)

Overload of the constructor.

Parameters
(x0,y0,z0)Position of the origin of the fluid domain
(dx0,dy0,dz0)Spatial discretization step
(Nx0,Ny0,Nz0)Number of fluid cells in the x, y et z directions.
Grille::~Grille ( )

Destructor.

Member Function Documentation

void Grille::affiche ( )

Test display.

void Grille::affiche ( string  r)

Test display.

void Grille::BC ( )

Boundary conditions.

Types of BC: 1 = reflecting; 2 = periodic; 3= outflow.

Returns
void
void Grille::cells_intersection_face ( int &  in,
int &  jn,
int &  kn,
int &  in1,
int &  jn1,
int &  kn1,
std::vector< Bbox > &  box_cells,
std::vector< Cellule > &  Cells 
)

List of fluid cells intersected by an interface triangle between times t-dt and t.

Let $ C_1= grille[in][jn][kn]$ the cell where the interface triangle lies at time t and $ C_2= grille[in1][jn1][kn1]$ the cell where it lies at time t-dt.
Due to the fluid CFL condition, 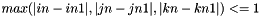$ max(|in-in1 |, |jn-jn1 |, |kn-kn1 |)<=1 $. There are therefore at most 8 cells intersected by the prism with bases the interface triangle at times t-dt (Particule.triangles_prev) and t (Particule.triangles) ):

  • $ grille[in][jn][kn]$
  • $ grille[in1][jn][kn]$
  • $ grille[in][jn1][kn]$
  • $ grille[in][jn1][kn1]$
  • $ grille[in1][jn1][kn]$
  • $ grille[in1][jn][kn1]$
  • $ grille[in][jn1][kn1]$
  • $ grille[in1][jn1][kn1]$
    Parameters
    (in,jn,kn)index of a Cellule (cell where the interface triangle lies at time t-dt (Particule.triangles_prev))
    (in1,jn1,kn1)index of a Cellule (cell where the interface triangle lies at time t (Particule.triangles))
    box_cellsvector of Box_3
    Cellsvector of Cellule
    Warning
    Specific coupling procedure !
    Returns
    void
Cellule Grille::cellule ( int  i,
int  j,
int  k 
)

Access cell (i,j, k).

Parameters
(i,j,k)index of the cell
Returns
Cellule
Cellule Grille::cible ( const Cellule &  c,
std::vector< std::vector< int > > &  tab_cible 
)
void Grille::corentx ( double  sigma)

Entropy correction in the x direction.

Parameters
sigma= dt/dx : time-step/ spatial discretization step for the fluid in the x direction
Returns
void
void Grille::corenty ( double  sigma)

Entropy correction in the y direction.

Parameters
sigma= dt/dy : time-step/ spatial discretization step for the fluid in the y direction
Returns
void
void Grille::corentz ( double  sigma)

Entropy correction in the z direction.

Parameters
sigma= dt/dz : time-step/ spatial discretization step for the fluid in the z direction
Returns
void
double Grille::Energie ( )

Computation of the total fluid energy.

Returns
double
void Grille::Fill_cel ( Solide &  S)

Filling of the ghost cells (alpha = 1)

In order to compute the fluxes at the fluid-solid interface, we define a fictitious state in the cells fully occupied by solid (alpha = 1), which is taken equal to the state in the mirror cell with regards to the boundary.
Algorithm: search for the interface closest to the center of the cell (loop on all solid faces) and compute the projection of the cell center on this interface using function CGAL::projection(Point_3) .

Parameters
SSolid
Warning
Specific coupling procedure !
Returns
void
void Grille::fnumx ( const double  sigma,
double  t 
)

Computation of the numerical x-flux.

Parameters
sigma= dt/dx: time-step/fluid spatial discretization step in the x direction
tcurrent simulation time
Returns
void
void Grille::fnumy ( const double  sigma,
double  t 
)

Computation of the numerical y-flux.

Parameters
sigma= dt/dy: time-step/fluid spatial discretization step in the y direction
tcurrent simulation time
Returns
void
void Grille::fnumz ( const double  sigma,
double  t 
)

Computation of the numerical z-flux.

Parameters
sigma= dt/dz: time-step/fluid spatial discretization step in the x direction
tcurrent simulation time
Returns
void
void Grille::Forces_fluide ( Solide &  S,
const double  dt 
)

Computation of fluid forces (Particule.Ff) and torques (Particule.Mf) applied on the Solide.

Let f an interface element, the pressure force exerted by the fluid on interface f is given by:

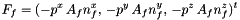
\begin{eqnarray*} F_f = (- p^x \, A_f n^{x}_f, \,- p^y \,A_f n^{y}_f, \,- p^z \,A_f n^{z}_f )^t \end{eqnarray*}


where 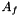$ A_f $ is the area of interface f, 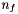$ n_f $ the exterior normal to f, and 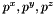$ p^x, p^y, p^z $ are the effective pressures in the x, y and z directions during the time-step (Cellule.pdtx, Cellule.pdty and Cellule.pdtz). The fluid torque exerted on f is given by:

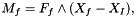
\begin{eqnarray*} M_f = F_f \wedge (X_f - X_I), \end{eqnarray*}

where 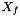$ X_f $ is the center of interface f and 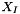$ X_I $ is the center of the particle containing f. These forces are transmitted to the solid as being constant during the time-step.

Parameters
SSolid
dtTime-step
Warning
Specific coupling procedure !
Returns
void
void Grille::Impression ( int  n)

Print out results.

Parameters
nindex of the output file
Returns
void
double Grille::Impulsionx ( )

Computation of the total fluid x-momentum.

Returns
double
double Grille::Impulsiony ( )

Computation of the total fluid y-momentum.

Returns
double
double Grille::Impulsionz ( )

Computation of the total fluid z-momentum.

Returns
double
Cellule Grille::in_cell ( const Point_3 &  p)

Access the cell containing point p.

Parameters
pa point
Returns
Cellule (cell containing p)
void Grille::in_cell ( const Point_3 &  p,
int &  i,
int &  j,
int &  k,
bool &  interieur 
)

Access cell containing point p.

Parameters
pa point
(i,j,k)index of the cell containing point p
interieur= true if point p is inside the fluid domain, false otherwise
Returns
void
void Grille::Init ( )

Definition of initial conditions.

Returns
void
std::vector<Point_3> Grille::intersection ( Triangle_3  t1,
Triangle_3  t2 
)
double Grille::Masse ( )

Computation of the total fluid mass.

Returns
double
void Grille::melange ( const double  dt)

Mixing the cells with negative density or pressure with neighbours.

Parameters
dttime-step
Returns
void
void Grille::Mixage ( )

Conservative mixing of small cut-cells.

We define a small cut-cell as a cell such that 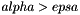$ alpha > epsa $ (Cellule.alpha solid occupancy ratio, and epsa: limit ratio for small cut-cells defined in parametres.hpp). In order not to modify the time-step which ensuring the CFL condition, the small cut-cells are merged with their neighbours. Denote p a small cut-cell and g a neighbouring cell such that g is totally fluid~( 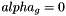$ alpha_g = 0 $ ). Define the following exchange terms:

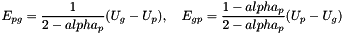
\begin{eqnarray*} E_{pg} = \frac{1}{2 - alpha_p} (U_g - U_{p}), \quad E_{gp} = \frac{1- alpha_p}{2 - alpha_p} (U_p - U_{g}) \end{eqnarray*}

and set:

\begin{eqnarray*} U_p = U_{p} + E_{pg}, \quad \quad U_g = U_{g} + E_{gp} \end{eqnarray*}

Warning
Specific coupling procedure !
Returns
void
void Grille::Mixage_cible ( )

Conservative mixing of small cut-cells.

We define a small cut-cell as a cell such that 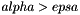$ alpha > epsa $ (Cellule.alpha si the solid occupancy ratio in the cell, and epsa is the maximum value accepted for CFL stability reasons and is set in parametres.hpp ). In order not to modify the time-step while keeping the original CFL condition, the small cut-cells are merged with their neighbours.

Warning
Specific coupling procedure !
Returns
void
bool Grille::Mixage_cible2 ( )

Conservative mixing of small cut-cells.

We define a small cut-cell as a cell such that 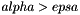$ alpha > epsa $ (Cellule.alpha si the solid occupancy ratio in the cell, and epsa is the maximum value accepted for CFL stability reasons and is set in parametres.hpp ). In order not to modify the time-step while keeping the original CFL condition, the small cut-cells are merged with their neighbours. This is an alternative version of Grille::Mixage_cible()

Warning
Specific coupling procedure !
Returns
void
void Grille::Modif_fnum ( const double  dt)

Modification of fluid fluxes and discrete balance on a cell (cut-cell method).

The fluid sees the presence of the solid through this function. The final value of the state 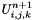$ U^{n+1}_{i, j, k}$ in the cell is computed using:

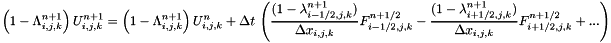
\begin{eqnarray*} \left( 1- \Lambda_{i,j,k}^{n+1} \right) U^{n+1}_{i,j,k} = \left( 1- \Lambda_{i,j,k} ^{n+1}\right) U^n_{i,j,k} + \Delta t \, \left( \frac{(1-\lambda_{i-1/2,j,k}^{n+1} )}{\Delta x_{ i,j,k}} F_{i-1/2, j, k}^{n+1/2} -\frac{(1-\lambda_{i+1/2,j,k}^{n+1} )}{\Delta x_{ i,j,k}} F_{i+1/2, j, k}^{n+1/2} + ...\right) \end{eqnarray*}

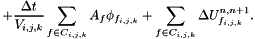
\begin{eqnarray*}+ \frac{\Delta t}{V_{i,j,k}} \sum_{f \in C_{i,j,k}}{A_{f}} {\phi}_{f_{ i,j,k}} + \sum_{f \in C_{i,j,k}} \Delta U^{n, n+1}_{f_{ i,j,k}} . \end{eqnarray*}

where 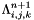$ \Lambda_{i,j,k}^{n+1} $: Cellule.alpha (solid occupancy ratio in cell (i,j,k)),
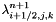$ \lambda_{i+1/2,j,k}^{n+1} $: Cellule.kappai (solid occupancy ratio on the faces of cell (i,j,k)),
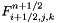$ F_{i+1/2, j, k}^{n+1/2} $: Cellule.fluxi (flux to the right of cell (i,j,k)),
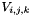$ V_{i,j,k} $: volume of cell (i,j,k),

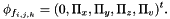
\begin{eqnarray*} \phi_{f_{ i,j,k}} = (0, \Pi_x, \Pi_y,\Pi_z, \Pi_v)^t. \end{eqnarray*}

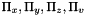$ \Pi_x, \Pi_y,\Pi_z, \Pi_v$: Cellule.phi_x, Cellule.phi_y, Cellule.phi_z, Cellule.phi_v (boundary fluxes),
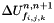$ \Delta U^{n, n+1}_{f_{ i,j,k}} $: Cellule.delta_w (swept quantity).

Parameters
dtTime-step
Warning
Specific coupling procedure !
Returns
void
void Grille::Parois_particles ( Solide &  S,
double  dt 
)

Intersection of the fluid grid with solid.

Intersection of the fluid grid with the solid and computation of the quantities of interest: solid occupancy ratio in the cell (Cellule.alpha), solid occupancy ratio on the cell faces (Cellule.kappai, Cellule.kappaj and Cellule.kappak). Definition of the interface objects:

  • Particule.Points_interface: intersection points of the cell with the triangular faces of the solid;
  • Particule.Triangles_interface: partition of the solid faces into interface triangles contained in one single cell of the fluid grid;
  • Particule.Position_Triangles_interface: index of the fluid grid cell containing Particule.Triangles_interface.
    Algorithm:
  • Construct vector box_grille containing the cubic cells of the fluid grid in the form of 3d bounding boxes (Bbox).
  • Construct the vector solide of the bounding boxes associated with the Particule.
  • Loop on box_grille.
  • Loop on solide.
  • Test the intersection between box_grille and solide using function CGAL::do_overlap(Bbox, Bbox). If so:
  • Test whether box_grille is fully contained in solide via la fonction box_inside_convex_polygon(const Particule&, const Bbox&). If so, the intersection is box_grille. Otherwise:
  • Browse the solid vertices contained in box_grille
  • Intersect the edges of box_grille with the solid faces
  • Loop on the triangular faces of the Solide.
  • Browse the vertices of the triangular faces of Solide contained in box_grille using function inside_box(const Bbox&, const Point_3&).
  • Test the intersections between box_grille and the triangular faces of Solide using function CGAL::do_intersect(Bbox,Triangle_3). If so:
  • Triangulate the faces of box_grille using function triang_cellule(const Bbox&, Triangles&) .
  • Loop on the triangular faces of box_grille.
  • Browse the vertices of the faces of box_grille contained in Solide using function inside_convex_polygon(const Particule&, const Point_3&).
  • Test the intersection between the faces of box_grille and the triangular faces of Solide (Particule.triangle) using function CGAL::do_intersect(Triangle_3, Triangle_3). If so:
  • Compute the intersection between the triangular faces of box_grille and the triangular faces of Solide using function CGAL::intersection(Triangle_3, Triangle_3).
Remarks
The vector Particule.Points_interface containing the intersection points between fluid cells and triangular faces (Particule.triangles) is progressively filled during the intersection algorithm.
The intersection result is used to compute the interest quantities Cellule.alpha, Cellule.kappai, Cellule.kappaj and Cellule.kappak.
The function used in the intersection computation are CGAL::Triangulation(vector<Point_3>) , CGAL::convex_hull_3(vector<Point_3>, Polyhedron_3) , CGAL::tetrahedron.volume() and CGAL::Triangle_3.squared_area().
Parameters
SSolide
dtTime-step
Warning
Specific coupling procedure !
Returns
void
double Grille::pas_temps ( double  t,
double  T 
)

Computation of the fluid time-step.

Parameters
Ttotal simulation time
tcurrent simulation time
Returns
double
void Grille::Solve ( const double  dt,
double  t,
int  n,
Solide &  S 
)

Resolution of the fluid equations.

Directional (Strang) splitting at each time-step.

Parameters
tCurrent simulation time
dtTime-step
nindex of the time iterations
Returns
void
void Grille::solve_fluidx ( const double  dt)

Solve the fluid equations in the x direction.

Warning
Storage of the pressure used during the time-step pdtx . Specific coupling parameter !
Parameters
dttime-step
Returns
void
void Grille::solve_fluidy ( const double  dt)

Resolution of fluid equations in the y direction.

Warning
Storage of the pressure used during the time-step pdty . Specific coupling parameter !
Parameters
dttime-step
Returns
void
void Grille::solve_fluidz ( const double  dt)

Resolution of the fluid equations in the z direction.

Warning
Storage of the pressure used during the time-step pdtz . Specific coupling parameter !
Parameters
dttime-step
Returns
void
void Grille::Swap_2d ( const double  dt,
Solide &  S 
)

Computation of the quantity of fluid swept by the solid between times t-dt and t.

Algorithm:

  • Split the solid faces (Particule.triangles and Particule.triangles_prev) into triangles fully contained in one single cell at times t-dt and t (not necessarily the same cell) using function sous_maillage_faceTn_faceTn1_2d(Triangle_3&, Triangles&, Triangle_3&, Triangles&, Vector_3& ,Triangles& ,Triangles&).
  • Compute the swept quantity and the boundary flux using function swap_face(Triangles&, Triangles&, const double , Particule &).
    Warning
    Specific coupling procedure !
    Parameters
    SSolide
    dtTime-step
    Returns
    void
void Grille::Swap_3d ( const double  dt,
Solide &  S 
)
void Grille::swap_face ( const Triangles &  T3d_prev,
const Triangles &  T3d_n,
const double  dt,
Particule &  P,
double &  volume_test 
)

Computation of the quantity of fluid swept by an interface triangle between t-dt and t, and computation of the boundary flux.

Algorithm:

  • Construction of the Box vector containing the prisms with bases T3d_prev and T3d_n. Loop on the prisms obtained:
  • We look for the indices of the cells containing T3d_prev (constructed to be fully contained in one cell) and T3d_n (idem).
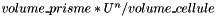  • If the prism is contained in one single cell, compute the volume of the prism using function volume_prisme(const Triangle_3&,const Triangle_3&), and the swept quantity for the interface triangle Particule.triangles is given by: $ volume\_prisme*U^n/volume\_cellule $. Otherwise,
  • List the fluid cells intersected by the prism using function cells_intersection_face(int& ,int& ,int& ,int& ,int& ,int& , std::vector<Bbox>& s, std::vector<Cellule>& s).
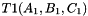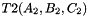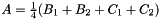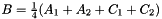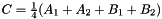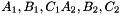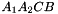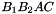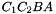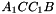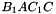  • Split the prism into tetrahedra: let $ T1(A_1,B_1,C_1)$ and $ T2(A_2,B_2,C_2)$ the prism bases, define points: $ A = \frac{1}{4}(B_1 + B_2 + C_1 +C_2) $ , $ B = \frac{1}{4}(A_1 + A_2 + C_1 +C_2) $ and $ C = \frac{1}{4}(A_1 + A_2 + B_1 + B_2 ) $. 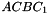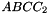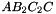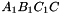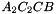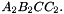The prism is split into the tetrahedra $ A_1,B_1,C_1 A_2,B_2,C_2 $ sont: $ A_1 A_2 C B $, $ B_1 B_2 A C $, $ C_1 C_2 B A $, $ A_1 C C_1 B $, $ B_1 A C_1 C $, $ A C B C_1 $, $ A B C C_2 $, $ A B_2 C_2 C $, $ A_1 B_1 C_1 C $, $ A_2 C_2 C B $, $ A_2 B_2 C C_2. $
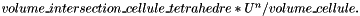
  • Intersect these tetrahedra with the fluid cells intersected by the prism using function intersect_cube_tetrahedron(Bbox&, Tetrahedron&). The swept quantity for the interface triangle is given by the sum of the following quantities: $ volume\_{intersection\_cellule\_tetrahedre}*U^n/volume\_cellule. $
    Computation of the boundary fluxes: let f an interface triangle, the boundary flux is given by:

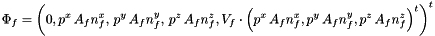
    \begin{eqnarray*} \Phi_f = \left(0, p^x \, A_f n^{x}_f, \, p^y \,A_f n^{y}_f, \, p^z \,A_f n^{z}_f, V_f \cdot \left( p^x \, A_f n^{x}_f,p^y \,A_f n^{y}_f,p^z \,A_f n^{z}_f \right)^t \right)^t \end{eqnarray*}


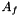    where $ A_f $ is the area of f, 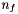$ n_f $ is the exterior normal to f, 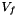$ V_f $ is the velocity at the center of f computed with function vitesse_parois(Point_3& ) and 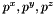$ p^x, p^y, p^z $ are the effective pressures in the x, y and z direction during the time-step (Cellule.pdtx, Cellule.pdty and Cellule.pdtz).
Parameters
T3d_prevTriangles_3 (interface triangles at time t: Particule.Triangles_interface)
T3d_nTriangles_3 (interface triangles at time t-dt: Particule.Triangles_interface_prev)
dtTime-step
PParticule
Warning
Specific coupling procedure !
Returns
void
void Grille::swap_face_inexact ( const Triangle_3 &  Tr_prev,
const Triangle_3 &  Tr,
const Triangles &  T3d_prev,
const Triangles &  T3d_n,
const double  dt,
Particule &  P,
double &  volume_test 
)

Computation of the swept quantity for an interface triangle between times t-dt and t. Computation of the boundary flux.

Algorithm:

  • Construction of the vector of the bounding boxes of the prisms with bases T3d_prev and T3d_n. Loop on the prisms obtained:
  • Look for the indices of the cells containing T3d_prev (due to the construction, the triangle is fully contained in one single cell) and T3d_n (idem).
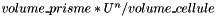  • If the prism is contained in one single cell, compute the prism volume using function volume_prisme(const Triangle_3&,const Triangle_3&), and the quantity swept by the interface triangle (Particule.triangles) is given by: $ volume\_prisme*U^n/volume\_cellule $. Otherwise,
  • List fluid cells intersecting the prism using function cells_intersection_face(int& ,int& ,int& ,int& ,int& ,int& , std::vector<Bbox>& s, std::vector<Cellule>& s).
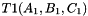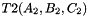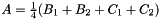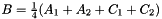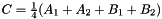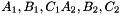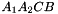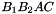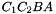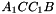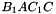  • Split the prism into tetrahedra: let $ T1(A_1,B_1,C_1)$ and $ T2(A_2,B_2,C_2)$ the prism bases, and define points: $ A = \frac{1}{4}(B_1 + B_2 + C_1 +C_2) $ , $ B = \frac{1}{4}(A_1 + A_2 + C_1 +C_2) $ et $ C = \frac{1}{4}(A_1 + A_2 + B_1 + B_2 ) $. 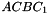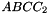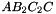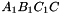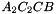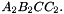The prism is split into the prisms $ A_1,B_1,C_1 A_2,B_2,C_2 $ sont: $ A_1 A_2 C B $, $ B_1 B_2 A C $, $ C_1 C_2 B A $, $ A_1 C C_1 B $, $ B_1 A C_1 C $, $ A C B C_1 $, $ A B C C_2 $, $ A B_2 C_2 C $, $ A_1 B_1 C_1 C $, $ A_2 C_2 C B $, $ A_2 B_2 C C_2. $
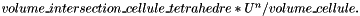
  • Intersection of these tetrahedra with the fluid cells intersected by the prism using function intersect_cube_tetrahedron(Bbox&, Tetrahedron&). The quantity swept by the interface triangle is given by the sum of the following terms: $ volume\_{intersection\_cellule\_tetrahedre}*U^n/volume\_cellule. $
    Computation of the boundary flux: let f an interface triangle, the boundary flux is given by:

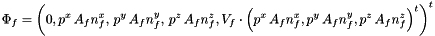
    \begin{eqnarray*} \Phi_f = \left(0, p^x \, A_f n^{x}_f, \, p^y \,A_f n^{y}_f, \, p^z \,A_f n^{z}_f, V_f \cdot \left( p^x \, A_f n^{x}_f,p^y \,A_f n^{y}_f,p^z \,A_f n^{z}_f \right)^t \right)^t \end{eqnarray*}


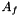    where $ A_f $ is the area of f, 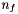$ n_f $ is the exterior normal to f, 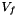$ V_f $ is the velocity at the center of f computed using function vitesse_parois(Point_3& ) and 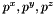$ p^x, p^y, p^z $ are the effective pressures in the directions x, y and z during the time-step (Cellule.pdtx, Cellule.pdty et Cellule.pdtz).
Parameters
T3d_prevTriangles_3 (interface triangles at time t: Particule.Triangles_interface)
T3d_nTriangles_3 (interface triangles at time t-dt: Particule.Triangles_interface_prev)
dtTime-step
PParticule
Warning
Specific coupling procedure !
Returns
void
Cellule Grille::voisin ( const Cellule &  c)
Cellule Grille::voisin_fluide ( const Cellule &  c,
bool &  target 
)
Cellule Grille::voisin_mixt ( const Cellule &  c,
bool &  target 
)

Field Documentation

double Grille::dx

Spatial discretization step.

double Grille::dy
double Grille::dz
vector< vector< vector<Cellule > > > Grille::grille

Fluid mesh.

double Grille::x

Position of the origin of the fluid grid.

double Grille::y
double Grille::z
The documentation for this class was generated from the following files:
Generated by   doxygen 1.8.11