
- Economics
Optimal growth and consumption
Risk and Decision
Economics of Energy
- Minimisation de coûts d'abattement de gaz à effet de serre
- Scénarios de pénétration du véhicule électrique et calcul de valeurs d'option
The Newsvendor Problem
Harry Markowitz publicó en 1952 un artículo titulado Portfolio Selection en el Journal of Finance, en el que estudiaba el proceso de selección de un portafolio de inversión (Markowitz, 1959). De acuerdo con Markowitz, el proceso de selección de un portafolio consta de dos etapas. La primera comienza con la observación y la experiencia, y termina con las expectativas del comportamiento futuro de los valores. La segunda etapa comienza con las expectativas y finaliza con la selección del portafolio. El artículo de Markowitz se ocupa de estudiar la segunda parte del proceso de la selección de un portafolio. Para seleccionar dicho portafolio se utilizara el concepto que propuso Markowitz, bajo la regla de ’valor esperado-varianza’ en la cual el decisor preferirá un proyecto A sobre un proyecto B si alguna de estas afirmaciones es válida:
Y en donde un conjunto de activos de inversión tendrían infinidad de proporciones para configurarse, que al limitarse forman lo que se conoce como una frontera eficiente. Una ampliación de esta teoría fue desarrollado por Van Horne (Horne, 1997) y a Myers (Myers, 1996), entre otros.
De forma matemática (Modigliani, 2009), el problema abordado por Markowitz consistía entonces en determinar el portafolio que minimizara la varianza total, sujeto a un nivel de rentabilidad preestablecido, y que la suma de las proporciones de cada una de las acciones sumara uno, tal como se muestra a continuación:
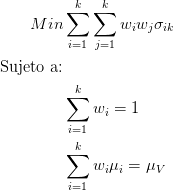
Donde: k: Numero de activos en el portafolio
wi: Peso correpondiente al activo i en el portafolio
σik: Covarianza de las activos i y j
μi: Retorno promedio del activo i
μV : Retorno promedio del portafolio
Dado una la serie de tiempo de k activos, como la que se muestra a continuación:
Los datos completos se encuentran en el archivo retornos.csv, que corresponden a 7 activos y 60 periodos, en este caso días. Para cargar el archivo en Scicolab use:
Para calcular el promedio de rendimiento y la matriz de covarianza para k activos use las siguientes lineas de comando de Scicoslab:
Pregunta 1 ¿Cúal de los 7 activos tiene mayor rendimiento promedio?
¿Cúal de los 7 activos tiene menor rendimiento promedio?
¿Cúal de los 7 activos tiene mayor riesgo?
¿Cúal de los 7 activos tiene menor riesgo?
El valor esperado de los retornos μV = E(KV ) y la varianza σV 2 = V ar(K V ) de un portafolio con pesos w esta dado por:
Donde: m es el vector de promedios de los activos y C es la matriz de covarianzas de los
activos
La siguiente función en Scicoslab calcula el valor esperado y varianza de un portafolio dado, las entrada son: el vector con los pesos del portafolio, el vetor de retornos promedios y a matriz de covarianza, devuelve el retorno promedio y la varianza del portafolio.
Pregunta 2 Construye un portafolio w que de el mismo peso a los activos identificados en
la pregunta 1. ¿Cúal es el promedio y la varianza de ése portafolio?
El portafolio con varianza mínima en el conjunto posible esta definido por los siguientes pesos:
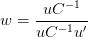 | (3) |
Donde u = [1 1 1 1] con k columnas, correspondiente al número de activos del
portafolio
1] con k columnas, correspondiente al número de activos del
portafolio
La siguiente función en Scicoslab calcula el Portafolio de Varianza Mínima, la entrada es la matriz de covarianza, devuelve los pesos del portafolio de varianza mínima.
Pregunta 3 ¿Cúal es el Portafolio de Varianza Mínima dada la canasta de los 7 activos
del archivo retornos?
¿Qué peso tiene en el portafolio el activo de mayor riesgo?
¿Qué peso tiene en el portafolio el activo de mayor retorno?
¿Cúal es el retorno promedio y la varianza del Portafolio de Varianza Mínima?
La cartera con la menor varianza entre las carteras alcanzables con retorno esperado μV tiene los siguientes pesos:
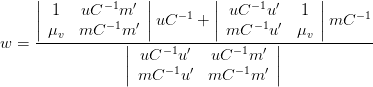 | (4) |
La siguiente función en Scicoslab calcula La cartera con la menor varianza entre las carteras alcanzables con un retorno esperado μV dado. Las entradas son: retorno esperado μV , vector de promedios de rendimiento de activos y la matriz de covarianza, devuleve los pesos del portafolio de varianza mínima dado el retorno esperado.
Pregunta 4 ¿Cúal es el Portafolio de Varianza Mínima para un portafolio con retorno
esperado igual al rendimiento promedio más alto de los 7 activos?
¿Cúal es la varianza de ése portafolio? comparalá con la varianza del activo de rendimiento
más alto. ¿Qué se puede concluir al respecto?
Para construir la frontera eficiente de Markowitz se deben integrar las funciones construidas en un script como el siguiente.
Pregunta 5 Construya la frontera eficiente dada la canasta de los activos que contiene el
archivo retornos.
Identifique en el gráfico el promedio y la varianza de los cuatro activos identificados en la
pregunta 1. ¿Cúales son eficientes?
Identifique en el gráfico el promedio y la varianza del portafolio de la pregunta 2. ¿És
eficientes?