La croissance optimale en économie
Les questions

J.-C. Péreau, L. Doyen, M. de Lara
(last modiﬁcation date: October 10, 2017)

Version pdf de ce document
Version sans bandeaux

1 Présentation du problème
2 Résolution analytique
3 Application numérique sous Scilab
4 Le modèle de Ramsey avec pollution

1 Présentation du problème
2 Résolution analytique
2.1 Horizon ﬁni
2.2 Horizon inﬁni
3 Application numérique sous Scilab
4 Le modèle de Ramsey avec pollution

1 Présentation du problème

On considère une économie dont l’objet est l’étude de l’accumulation du capital et de la consommation. Ce problème de croissance se pose dans les termes suivants : un planiﬁcateur a pour tâche de décider ce que les agents vont consommer et ce qu’ils vont ajouter au stock de capital en vue d’une consommation future plus importante. On suppose donc qu’il existe un bien unique pouvant être utilisé à la fois comme bien de consommation et de capital.

L’objectif du planiﬁcateur est de maximiser la somme actualisée des utilités de consommation par tête à chaque période. Sa fonction objectif s’écrit

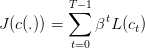T∑− 1 J(c(.)) = βtL(ct) t=0

(1)

où

c_t est la consommation à l’instant t ;
T < +∞ ou T = +∞ est l’horizon ;
β ∈]0, 1] est le taux d’actualisation (plus β est grand, plus l’utilité future décroît rapidement, soit encore plus les agents sont impatients).

L’égalité emploi-ressource s’écrit

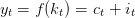yt = f(kt) = ct + it

(2)

où

k_t est le capital à l’instant t ;
i_t est l’investissement brut à l’instant t ;
f est la fonction de production ;
y_t est la production à l’instant t.

L’évolution du capital ou investissement net est donnée par

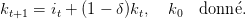kt+1 = it + (1 − δ)kt, k0 donn ´e.

(3)

Le coeﬃcient δ (0 ≤ δ ≤ 1) est le taux de dépréciation physique du capital.

La variable i_t ne joue qu’un rôle d’intermédiaire, et on obtient le modèle dynamique

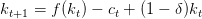kt+1 = f(kt) − ct + (1 − δ)kt

(4)

de variable d’état le capital k et de variable de commande la consommation c.

2 Résolution analytique

2.1 Horizon ﬁni

Cas de dépréciation totale du capital (δ = 1)

On prend δ = 1 et T < +∞, de sorte que le problème d’optimisation est

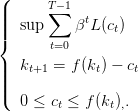( T−1 ||| ∑ t ||{ sup β L(ct) t=0 || kt+1 = f(kt) − ct |||( 0 ≤ ct ≤ f(kt),.

(5)

Question 1 Écrire le Hamiltonien H(k,c,p,t) du problème. En déduire, à l’aide du principe du minimum, les conditions nécessaires d’optimalité d’une trajectoire (k^♯(.),c^♯(.)).

Question 2 Écrire l’équation de Bellman. En déduire des feedbacks optimaux aux temps T − 1 et T − 2.

On suppose que la fonction de production est concave, de type Cobb-Douglas, et que la fonction d’utilité est logarithmique :

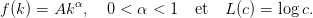α f (k ) = Ak , 0 < α < 1 et L(c) = logc.

(6)

Le coeﬃcient 0 < α < 1 est l’élasticité de la production par rapport au capital, et A > 0 est un paramètre d’échelle.

Question 3 Trouver une règle de décision optimale valable pour tous les temps inférieurs à T − 2. Déterminer la trajectoire optimale k^♯(.) correspondante. Que dire du taux d’épargne

def k♯t+1 zt = ----♯-α? A (kt)

(7)

Cas général

Le problème d’optimisation est

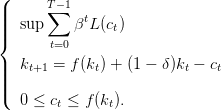( T− 1 ||| ∑ t ||{ sup β L (ct) t=0 || kt+1 = f (kt) + (1 − δ)kt − ct ||| ( 0 ≤ ct ≤ f (kt).

(8)

Question 4 Que change le paramètre δ dans les équations précédentes ?

2.2 Horizon inﬁni

On introduit le Lagrangien :

∞ ∞ def ∑ t ∑ t ℒ (c(.),k(.),λ(.)) = β L (ct) + β λt[f(kt) − ct − kt+1 + (1 − δ)kt]. t=0 t=0

(9)

On note que β^tλ_t joue le rôle de p_t (état adjoint).

Question 5 Montrer, en dérivant le Lagrangien par rapport à c(.),k(.), qu’une trajectoire optimale c^♯(.),k^♯(.) vériﬁe la condition dite de Keynes-Ramsey :

L ′(c♯t) ′ ♯ --′-♯--- = β[f (kt+1 ) + 1 − δ]. L (ct+1)

(10)

Cette condition d’optimalité caractérise le comportement optimal de consommation et d’épargne.

La fonction de production est toujours supposée de type Cobb-Douglas

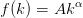α f(k) = Ak

(11)

et la fonction d’utilité des ménages est de forme iso-élastique avec γ l’inverse de l’élasticité de substitution intertemporelle. Pour γ = 1 on obtient une fonction logarithmique.

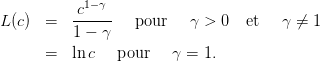
c1−γ L(c) = ------ pour γ > 0 et γ ⁄= 1 1 − γ = ln c pour γ = 1.

Question 6 Que devient la condition dite de Keynes-Ramsey ?

Question 7 Montrer, que pour δ = 1 et γ = 1, on a

c♯t lim --♯--α-= 1 − αβ. t→+ ∞ (kt+1 )

(12)

Question 8 Trouver une solution stationnaire (c^♯,k^♯).

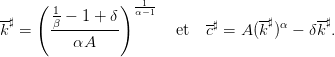( 1 ) α1−1 -♯ β-−-1-+-δ- -♯ -♯ α -♯ k = αA et c = A(k ) − δk .

(13)

3 Application numérique sous Scilab

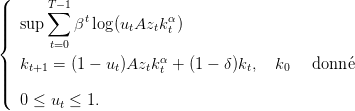( || T∑− 1 ||| sup βtlog(utAztktα) { t=0 | k = (1 − u )Az kα + (1 − δ)k , k donn ´e ||| t+1 t tt t 0 |( 0 ≤ ut ≤ 1.

(14)

Le terme z_t représente un choc de productivité,

Question 9 Recopier les paramètres suivants dans un ﬁchier Ramsey.sce. Donner les expressions de la solution stationnaire (c^♯,k^♯).

  // exec('Ramsey.sce');

  // Paramètres
  alpha=0.25;
  A=1;
  beta=0.98;
  delta= 0.05;
  T=20;

  function [z]=productivite(t), z=1, endfunction;
  //function [z]=productivite(t), ...
  //      if t <= 1, z=1, else z=1.99, end, endfunction;
  // choc de productivité

Question 10 Charger dynoptim et consulter le help. Déﬁnir la dynamique f et ses dérivées partielles f_k par rapport à l’état et f_u par rapport à la commande. Faire de même avec le coût instantané et le coût ﬁnal. Écrire les contraintes sur les commandes.

Question 11 Choisir un capital initial k0 (plus ou moins proche de la solution stationnaire). Initialiser l’algorithme d’optimisation dynamique dynoptim avec un vecteur u_init. Faire un appel à dynoptim et tracer les solutions. Vériﬁer que les solutions coïncident avec celles des Questions précédentes.

Question 12 Que constatez-vous en faisant varier le facteur d’actualisation β ?

Question 13 Que constatez-vous en faisant varier l’horizon T ?

Question 14 Changer la fonction d’utilité log en une fonction du type iso-élastique. Que se passe-t-il si γ → 1 ?

Question 15 Envisager un choc de productivité.

4 Le modèle de Ramsey avec pollution

D’après F. Van der Ploeg et C. Withagen (1991) ”Pollution Control and the Ramsey Problem”, ERE, 1, pp:215-30.

Nous reprenons les équations du modèle de Ramsey et nous introduisons la dimension environnementale modélisée sous la forme d’un ﬂux de pollution intervenant en tant qu’externalité négative dans le fonction d’utilité des ménages. La pollution est donc un produit fatal de l’activité productive.

On supposera que la société est aﬀectée par la qualité de l’environnement à travers une fonction d’utilité log-log additivement séparable, croissante avec la consommation et décroissante avec la pollution modélisée sous forme de ﬂux. η_p > 0 mesure la désutilité de la pollution ou la préférence pour la qualité environnementale. Le dommage environnemental résulte de l’utilisation du capital dans la production du bien ﬁnal. Il peut être réduit par la mise en oeuvre de techniques d’abattement (Z) pour un K donné. On notera χ > 0 l’élasticité de la pollution par rapport au ratio capital physique/activités d’abattement (de réduction).

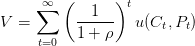
( ) ∑∞ 1 t V = ------ u(Ct,Pt) t=0 1 + ρ

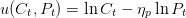
u(Ct,Pt) = ln Ct − ηplnPt

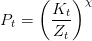
( ) χ P = Kt- t Zt

La contrainte emploi-ressource devient

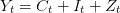
Yt = Ct + It + Zt

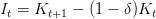
I = K − (1 − δ)K t t+1 t

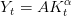
α Yt = AK t

Le lagrangien s’écrit :

∑∞ ( 1 )t max ℒ = ------ u (Ct,Pt) Ct,Kt+1,Zt t=0 1 + ρ ∑∞ ( )t + -1---- λ [Y − C − K + (1 − δ)K − Z ] 1 + ρ t t t t+1 t t t=0

avec k₀ donné. On en déduit les CPO :

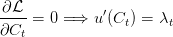
∂ ℒ ----= 0 = ⇒ u′(Ct ) = λt ∂Ct

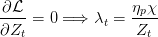
∂ ℒ ηpχ ----= 0 = ⇒ λt = ---- ∂Zt Zt

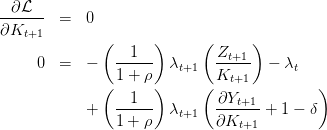
--∂ℒ-- ∂Kt+1 = 0 ( ) ( ) 0 = − --1--- λt+1 -Zt+1 − λt 1 + ρ Kt+1 ( 1 ) ( ∂Yt+1 ) + ------ λt+1 ------ + 1 − δ 1 + ρ ∂Kt+1

ce qui donne les deux conditions d’optimalité qui retracent le double arbitrage que fait face le planiﬁcateur entre d’une part l’arbitrage entre consommation présente et consommation future et d’autre part l’arbitrage intra période entre consommation et dépollution :

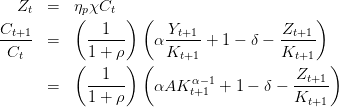
Zt = ηpχCt Ct+1 ( 1 ) ( Yt+1 Zt+1) ----- = ------ α -----+ 1 − δ − ----- Ct ( 1 + ρ) ( Kt+1 Kt+1 ) --1--- α− 1 -Zt+1 = 1 + ρ αAK t+1 + 1 − δ − K t+1

Ces conditions signiﬁent qu’à l’optimum, le renoncement à une unité de consommation doit être exactement compensée par le gain d’utilité procurée par la baisse de la pollution et que l’utilité marginale anticipée du renoncement à une unité de consommation destinée à l’accumulation du capital physique doit exactement couvrir la perte marginale d’utilité qu’implique ce renoncement. À l’état stationnaire, il vient :

( ) ss (1 + ηpχ )ρ + δ 1∕(α−1) K = -------------------- Ax [ηpχα(α − 1) + α ] Y ss = Ax (Kss) ( 1 ) Css = -------- (A (Kss)α − δKss ) 1 − ηpχ Zss = ηpχCss

On retient comme valeur des paramètres :

A	α	δ	η_p	ρ	χ
1	0.25	0.05	0.025	0.02	0.8

On peut alors envisager un choc sur η_p avec une nouvelle valeur de 0.05. Les paramètres η_p et χ sont posés de telle manière que Z∕Y = 1.6%.

Question 16 Programmer ce nouveau modèle avec Scilab, et étudier ses propriétés en simulation.

Formations

Départements

Pratique

Recherche

Optimal growth and consumption

Risk and Decision

Economics of Energy

The Newsvendor Problem

La croissance optimale en économie
Les questions

Contents

1 Présentation du problème

2 Résolution analytique

2.1 Horizon ﬁni

Cas de dépréciation totale du capital (δ = 1)

Cas général

2.2 Horizon inﬁni

3 Application numérique sous Scilab

4 Le modèle de Ramsey avec pollution

L'École des Ponts ParisTech est membre fondateur de	L'École des Ponts ParisTech est certifiée

Formations

Départements

Pratique

Recherche

Optimal growth and consumption

Risk and Decision

Economics of Energy

The Newsvendor Problem

La croissance optimale en économie Les questions

Contents

1 Présentation du problème

2 Résolution analytique

2.1 Horizon ﬁni

Cas de dépréciation totale du capital (δ = 1)

Cas général

2.2 Horizon inﬁni

3 Application numérique sous Scilab

4 Le modèle de Ramsey avec pollution

La croissance optimale en économie
Les questions