Fermer X

Investissement et gestion de patrimoine

Jonathan Boccara, Juliette de La Fabrègue et Olivier Dupont
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Introduction
2 Placements à capitalisation annuelle
3 Placement en bourse
4 Conclusion
A Annexe : Code spécifique pour le Livret A

Contents

1 Introduction
2 Placements à capitalisation annuelle
 2.1 Programme Scilab
 2.2 Livret A
 2.3 Assurance-vie
 2.4 Comparaison du livret A et de l’assurance-vie
3 Placement en bourse
 3.1 Obtention des variations mensuelles de l’indice CAC40
 3.2 Programme Scilab
 3.3 Simulation de différents placements en bourse
 3.4 Comparaison des trois différents placements
4 Conclusion
A Annexe : Code spécifique pour le Livret A
 A.1 Programme Scilab
 A.2 Exemple

1 Introduction

Le but de ce projet est de réaliser un logiciel de gestion de patrimoine, sous le logiciel scientifique Scilab, et de le mettre en libre accès sur Internet. L’intérêt de cette démarche réside dans la possibilté de modifier le code Scilab si besoin. Celui-ci consiste en quelques fonctions type, qui pourront être ensuite exploitées et modifiées selon les placements à modéliser, et sera disponible sur la page Internet.

Les différents types de placements ici traités sont principalement :

  • le livret A;
  • l’assurance-vie (monosupport en euros);
  • la bourse, le CAC40 étant pris comme référence.

Ces divers placements diffèrent essentiellement par le système de capitalisation des intérêts. Dans tous les cas, le calcul des intérêts s’effectue au mois, mais ils sont capitalisés soit en fin d’année, soit à la fin du mois. Ainsi, nous avons distingué, dans la structure même de ce projet, ces deux systèmes de capitalisation des intérêts.

2 Placements à capitalisation annuelle

Dans un placement financier à capitalisation annuelle, les intérêts sont bien calculés chaque mois, mais ne sont capitalisés qu’en fin d’année, de sorte qu’il n’y a pas d’intérêts sur les intérêts. On peut en revanche ajouter régulièrement de l’argent, ce qui a été pris en compte dans le programme associé à ce placement. Nous examinerons ensuite les cas du livret A et de l’assurance-vie.

2.1 Programme Scilab

Dans cette partie, on donne en Code Scilab 1 un programme définissant une fonction de nom annuel qui prend en arguments :

  • un vecteur contenant les taux du placement par mois ;
  • le montant du capital initial ;
  • le montant d’un éventuel apport régulier d’argent ;
  • les dates de dépôt et de retrait ;

et qui renvoie le capital final ainsi que les intérêts agrégés.

Cette fonction sera utilisée pour simuler des placements sur le livret A ainsi que sur l’assurance-vie.

Code Scilab 1.

//

function [capital,total_interets]=annuel(...  
tableau_taux,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin)  
// CAPITALISATION À LA FIN DE CHAQUE ANNÉE  
 
//error('Attention : mettre 4.5 pour un taux de 4,5 pourcent')  
//disp('Attention : mettre 4.5 pour un taux de 4,5 pourcent')  
 
capital=capital_initial;  
// vecteur des capitaux mois par mois  
total_interets=0;  
//interets cumules sur la duree du placement  
theta=tableau_taux/100/12;  
//taux mensuels avec 0 <= teta <= 1  
 
// ------------------------------------------------------------  
// Première année  
// ------------------------------------------------------------  
 
interets=0; // interets cumulés sur l'année  
 
if annee_fin>annee_debut  
  nb_mois_d=12-mois_debut;  
  // placement sur plus d'une année  
else nb_mois_d=mois_fin-mois_debut;  
  // placement au sein d'une même année  
end  
 
for j=1:nb_mois_d  
capital=[capital,capital($)+tableau_mensualites(j)];  
interets=interets+theta(j)*capital($);  
end  
// un montant placé le mois j est considéré comme rapportant  
// à partir du mois j+1  
// par exemple, un placement en décembre (mois_debut=12)  
// rapporte à partir de janvier de l'année suivante  
 
capital($)=capital($)+interets;  
total_interets=interets;  
 
 
// ------------------------------------------------------------  
// années intermédiaires  
// ------------------------------------------------------------  
 
if annee_fin>annee_debut+1  
  nb_annees=annee_fin-annee_debut-1;  
else nb_annees=0;  
end  
 
for i=1:nb_annees  
interets=0; // variable locale remise à zero à chaque début d'année  
for j=1:12  
  ind_mois=(i-1)*12+j+12-mois_debut ; // indice du mois en cours  
capital=[capital,capital($) + tableau_mensualites(ind_mois)];  
interets=interets+theta(ind_mois)*capital($);  
end  
capital($)=capital($)+interets;  
total_interets=total_interets+interets;  
end  
 
 
// ------------------------------------------------------------  
// dernière année  
// ------------------------------------------------------------  
 
if annee_fin>annee_debut  
//  nb_mois_f=mois_fin-1; //placement sur plus d'une année  
  nb_mois_f=mois_fin ;  
// else nb_mois_f=0;  
else nb_mois_f=0;  
end  
 
interets=0;  
 
for j=1:nb_mois_f  
  ind_mois=nb_mois_d+nb_annees*12+j ; // indice du mois en cours  
capital=[capital,capital($) + tableau_mensualites(ind_mois)];  
interets=interets+theta(ind_mois)*capital($);  
end  
 
capital($)=capital($)+interets;  
total_interets=total_interets+interets;  
 
endfunction  
 
// 

2.2 Livret A

Caractéristiques

Il s’agit ici de modéliser l’évolution d’un capital placé sur livret A, qu’on alimente tous les mois. On utilise dans ce but la fonction annuel définie plus haut. En effet, les intérêts ne sont capitalisés, dans le cas du livret A, qu’à la fin de chaque année. Toutefois, en toute rigueur, sur le livret A les intérêts sont calculés par quinzaines, et le livret A est plafonné : le code correspondant est donné en Annexe A.

Exemple

Un exemple d’application au livret A avec les données du Tableau 2.2 est donné en Code Scilab 2. On y traite simultanément le cas de taux stationnaire et de taux instationnaires. Les résultats sont présentés en Figure 2.2.

Code Scilab 2.

//

getf('annuel.sci');  
 
 
// -----------------------------------------------------------  
// Données communes  
// -----------------------------------------------------------  
 
mois_debut=05;  
annee_debut=1987;  
mois_fin=04;  
annee_fin=2007;  
mois=0:((12-mois_debut) + (annee_fin - annee_debut-1)*12 +...  
mois_fin);  
nb_mois=length(mois);  
 
capital_initial=1000;  
tableau_mensualite=100*ones(1,nb_mois);  
 
 
// ------------------------------------------------------------  
// Livret A  
// ------------------------------------------------------------  
 
taux_A=2.75;  
tableau_taux=taux_A*ones(1,nb_mois);  
 
[capital_A,total_interets_A]=annuel(...  
tableau_taux,capital_initial,tableau_mensualite,...  
mois_debut,annee_debut,mois_fin,annee_fin)  
 
 
// ------------------------------------------------------------  
// Graphiques  
// ------------------------------------------------------------  
 
xset('window',1); xbasc();  
 
plot2d2(mois,capital_A);  
 
xtitle('Livret A : Capital initial de' +...  
string(capital_initial) +' euros'+' et placements reguliers de '+...  
string(tableau_mensualite(1)) +' euros', 'Mois' ,'Capital');  
 
legends(['Livret A '+string(taux_A)+'%'],[1],'ul');  
 
//

PIC

Figure 1: Placement mensuel sur le livret A. Évolution du capital sur 10 ans.

Tauxdate d’entréedate de sortiemensualitécapital initial
2,75% 05/1987 04/2007 100 class="td11"> 1 000

Table 1: Données pour simulation de placement régulier sur le livret A

2.3 Assurance-vie

Caractéristiques

Nous allons maintenant procéder de la même manière pour un placement avec ajout mensuel, mais sur une assurance-vie. Nous avons choisi de modéliser un contrat monosupport en euros qui est le type de base de l’assurance-vie. Il existe également des contrats multisupports qui permettent de placer une partie du capital en bourse ou dans l’immobilier.

Le contrat monosupport en euros est un placement sans risque. Les versements sont soumis à des frais d’entrée. Les intérêts sont calculés mensuellement et capitalisés en fin d’année. Ces mêmes intérêts sont soumis aux prélèvements sociaux (11%). Au moment du retrait du capital, les intérêts sont soumis à l’impôt sur le revenu ou à un prélèvement libératoire forfaitaire de 7,5%. La somme à payer peut ensuite être déduite de l’impôt sur le revenu dans la limite de 4 600 class="umvs-x-x-120"> également des frais de gestion mais qui sont généralement déjà compris dans le taux annoncé.

Attention : pour bénéficier des avantages de l’assurance-vie décrits plus haut, il faut placer son argent pendant huit ans minimum. En effet, un retrait précoce entraine des frais de sortie très importants.

La fonction assurance_vie qui simule un placement en assurance-vie à partir de la fonction annuel est donnée en Code Scilab 3. La fonction ainsi définie prend en arguments :

  • un tableau contenant l’ensemble des taux mensuels (constants ici) appliqués tout au long de la période ;
  • le pourcentage prélevé par la banque à chaque versement ;
  • le montant du capital initial ;
  • le montant d’éventuels rajouts mensuels;
  • les dates d’entrée et de sortie ;

et renvoie la suite mensuelle des capitaux ainsi que le montant des intérêts agrégés.

Code Scilab 3.

//

 
//assurance-vie:contrat monosupport en euros  
 
function [capital,total_interets]=assurance_vie(tableau_taux,...  
   frais,capital_initial,tableau_rajouts,m1,a1,m2,a2)  
 
 
//frais: pourcentage prélevé par la banque sur chaque versement  
CS=0.89; //coefficient charges sociales  
 
t=tableau_taux*CS;  
C=capital_initial*(1-frais/100);  
R=tableau_rajouts*(1-frais/100);  
 
//getf('annuel.sci');  
 
[capital,total_interets]=annuel(t,C,R,m1,a1,m2,a2);  
 
//impot sur le revenu  
lim=4600; //limite de déduction fiscale  
p=0.075; //prelevement forfaitaire liberatoire  
 
if p*total_interets>lim  
capital($)=capital($)-p*total_interets+lim;  
total_interets=total_interets-p*total_interets+lim;  
 
end  
 
 
endfunction  
 
// 

Exemple

Un exemple d’utilisation relatif aux données du Tableau 2.3 est quant à lui fourni en Code Scilab 4. Les résultats sont présentés en Figure 2.3

Code Scilab 4.

//

taux=4.5;  
frais=3;  
capital_initial=1000;  
rajout=100;  
m1=05;  
a1=2007;  
m2=10;  
a2=2017;  
 
nb_mois=12-m1+(a2-a1)*12+m2;  
 
tableau_taux=taux*ones(1,nb_mois);  
tableau_rajouts=rajout*ones(1,nb_mois);  
 
getf('av2.sci');  
 
 [capital,total_interets]=assurance_vie(tableau_taux,frais, ...  
capital_initial,tableau_rajouts,m1,a1,m2,a2);  
 
xbasc();  
plot(capital);  
xtitle('Capital initial de'+...  
string(capital_initial) +' euros'+' et placements reguliers de'+...  
string(rajout)+'euros.','Mois', 'Capital');  
 
legends(['Assurance-vie '+string(taux)+'%, frais '+string(frais)+...  
 '% en entree'],[1},'ul');  
 
//

PIC

Figure 2: Assurance-vie : évolution du capital sur 10 ans

Tauxfraisdate d’entréedate de sortiemensualitécapital initial
4,5% 3 % 05/2007 10/2017 100 class="td11"> 1 000

Table 2: Données pour simulation de placement régulier sur l’assurance-vie

2.4 Comparaison du livret A et de l’assurance-vie

On dispose d’un bref historique des taux du livret A, donné en Tableau 2.4.

Date Taux
16 mai 1986 4,50 %
1er mars 19963,50 %
16 juin 1998 3,00 %
1er aout 19992,25 %
1er août 20052,00 %
1er août 20062,75 %

Table 3: Historique des taux du livret A

On peut donc comparer l’évolution d’un même capital pendant toute cette période, sur le livret A ou sur l’assurance-vie, en utilisant par exemple le Code Scilab 5

Code Scilab 5.

//

//getf('annuel.sci');  
 
 
// ------------------------------------------------------------  
// Données communes  
// ------------------------------------------------------------  
 
mois_debut=05;  
annee_debut=1986;  
mois_fin=04;  
annee_fin=2007;  
mois=0:((12-mois_debut) + (annee_fin - annee_debut-1)*12 +...  
mois_fin);  
nb_mois=length(mois);  
 
capital_initial=1000;  
tableau_mensualites=100*ones(1,nb_mois);  
 
 
// ------------------------------------------------------------  
// Livret A  
// ------------------------------------------------------------  
 
tableau_taux=[4.5*ones(1,118),3.5*ones(1,27),3*ones(1,14),...  
      2.25*ones(1,72),2*ones(1,12)];  
mois_restants=nb_mois-118-27-14-72-12;  
tableau_taux=[tableau_taux,2.75*ones(1,mois_restants)];  
 
[capital_A,total_interets_A]=annuel(...  
tableau_taux,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin);  
 
 
// ------------------------------------------------------------  
// Assurance-vie  
// ------------------------------------------------------------  
 
taux_av=4.5;  
frais=3;  
 
tableau_taux_av=taux_av*ones(1,nb_mois);  
 
//getf av2.sci;  
 
 [capital_av,total_interets_av]=assurance_vie(...  
 tableau_taux_av,frais,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin);  
 
// ------------------------------------------------------------  
// Graphiques  
// ------------------------------------------------------------  
 
 
xset('window',10); xbasc();  
 
plot2d2(mois,[capital_A ; capital_av]');  
 
xtitle('Capital initial de' +...  
string(capital_initial) +' euros'+' et placements reguliers de '+...  
string(tableau_mensualites(1)) +' euros', 'Mois' ,'Capital');  
 
legends(['Livret A (historique)' ; ...  
 'Assurance-vie '+string(taux_av)],[1,2],'ul');  
 
// 

Les résultats correspondants sont donnés en Figure 2.4.

PIC

Figure 3: Livret A et assurance-vie sur 10 ans

3 Placement en bourse

Il s’agit dans cette partie de pouvoir simuler des placements boursiers. Étant donnée une série (historique) de taux de rentabilité mensuels, ce placement s’apparente à une capitalisation mensuelle. Pour cette série historique, nous avons opté pour le CAC40. Nous disposons en effet de données relatives à l’indice CAC, ou son équivalent reconstitué, depuis 1965.

3.1 Obtention des variations mensuelles de l’indice CAC40

Les données relatives au CAC40 reconstitué peuvent être trouvées par exemple sur Internet http://jmrpassions.free.fr/bourse/cac40.php.

Une fois ces données saisies sous Scilab, le programme présenté en Code Scilab 6 permet de définir, pour chaque mois, le taux de rentabilité attaché à l’indice CAC40.

Code Scilab 6.

//

M=fscanfMat('cac40_mensuel.txt');  
Md=M(:,2); //Vecteur des valeurs en début de mois  
Mf=M(:,5); //Vecteur des valeurs en fin de mois  
tableau_taux_cac40=100* (Mf-Md)./Mf;  
//Vecteur des taux de variation pour chaque mois  
 
//

On peut alors représenter ces variations de taux sur un graphique donné en Figure 4.

PIC

Figure 4: Variation du taux de rémunération mensuelle de l’indice CAC40 reconstitué de janvier 1965 à juin 2003.

3.2 Programme Scilab

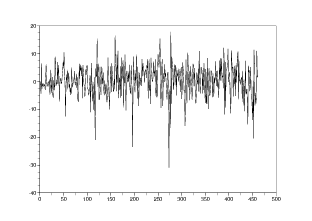
On définit dans cette section une fonction Scilab bourse qui permet de faire évoluer un capital selon les variations historiques du CAC40, ou d’autres indices pourvu que les données soient stockées dans un tableau. Elles est donnée en Code Scilab 7.

Cette fonction prend en arguments :

  • la date où commence le tableau historique ;
  • la suite des taux de rentabilité mensuels ;
  • la valeur du capital initial ;
  • la suite des apports mensuels ;
  • les dates de début et fin de placement,

et retourne la suite des valeurs mensuelles du capital, et le montant des plus-values.

Code Scilab 7.

//

function [capital,plus_values]=bourse(mois_tab,annee_tab,...  
tableau_taux,capital_initial,tableau_mensualites,mois_debut,...  
annee_debut,mois_fin,annee_fin)  
//mois_tab //mois de début du tableau des rentabilités  
//annee_tab //annee de début du tableau des rentabilités  
ind0=(12-mois_tab) + (annee_debut - annee_tab - 1)*12 +...  
mois_debut+1 ;  
indf=(12-mois_tab) + (annee_fin - annee_tab - 1)*12 +...  
mois_fin;  
 
capital=capital_initial;  
plus_values=0;  
cumul_mensualites=capital_initial;  
 
for k=ind0:indf  
  capital=[capital,capital($)*(1+tableau_taux(k)/100) +...  
   tableau_mensualites(k-ind0+1)];  
  //le tableau des mensualités n'est constitué que pour  
  //la période de placement... d'où l'indice.  
  cumul_mensualites=cumul_mensualites + tableau_mensualites(k-ind0+1) ;  
  plus_values=[plus_values, capital($) - cumul_mensualites ]  
end  
endfunction  
 
//

3.3 Simulation de différents placements en bourse

On donne dans la suite plusieurs exemples d’utilisation de la fonction bourse.

Evolution d’un capital brut placé en bourse

Le programme qui figure en Code Scilab 8 donne l’évolution d’un capital placé en bourse, si l’on n’apporte pas de mensualités. Le graphique qui en résulte est lui donné en Figure 5, et est relatif aux données du Tableau 3.3.

Code Scilab 8.

//

// ---------------------------------------------------------  
// Données  
// ---------------------------------------------------------  
 
mois_debut=01;  
annee_debut=1985;  
mois_fin=01;  
annee_fin=1995;  
 
mois=0:((12-mois_debut) + (annee_fin - annee_debut-1)*12 +...  
mois_fin);  
nb_mois=length(mois);  
 
capital_initial=1000;  
tableau_mensualites=zeros(1,nb_mois);  
 
// ---------------------------------------------------------  
 
exec taux_cac.sci ;  
tableau_taux=tableau_taux_cac40;  
 
getf bourse.sci  
mois_tab=01;  
annee_tab=1965;  
 
// --------------------------------------------------------------  
// --------------------------------------------------------------  
 
[capital_cac,plus_values_cac]=bourse(...  
mois_tab,annee_tab,tableau_taux,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin);  
 
// ------------------------------------------------------------  
// Graphique  
// ------------------------------------------------------------  
 
 
xset('window',1); xbasc();  
 
plot2d2(mois,capital_cac');  
 
xtitle('Capital initial de' +...  
string(capital_initial) +' euros'+' et placements reguliers de '+...  
string(tableau_mensualites(1)) +' euros', 'Mois' ,'Capital');  
 
legends(['Bourse de  '+string(mois_debut)+'/'+string(annee_debut)+...  
 '  a  '+string(mois_fin)+'/'+string(annee_fin)],[1],'ul');  
 
//

PIC

Figure 5: Evolution d’un capital en bourse sans apport mensuel

Date d’entréedate de sortiemensualitécapital initial
01/1985 01/1995 0 class="td11"> 1 000

Table 4: Données pour simulation de capital en bourse sans menusalité
Evolution du même capital avec apports mensuels

On aimerait ici confirmer ou infirmer la stratégie proposée par les banques qui consiste à préférer un apport régulier d’argent afin de ”lisser” les variations chaotiques des cours de la bourse. On va donc simuler le même placement que précédemment, mais en apportant régulièrement de l’argent. Le programme associé, peu différent du précédent, est donné en Code Scilab 9. Le graphique qui présente les deux courbes simultanément est celui de la Figure 6; il correspond aux données du Tableau 3.3.

Code Scilab 9.

//

// ---------------------------------------------------------  
// Données  
// ---------------------------------------------------------  
 
mois_debut=01;  
annee_debut=1985;  
mois_fin=01;  
annee_fin=1995;  
 
mois=0:((12-mois_debut) + (annee_fin - annee_debut-1)*12 +...  
mois_fin);  
nb_mois=length(mois);  
 
capital_initial=1000;  
tableau_mensualites=100*ones(1,nb_mois);  
tableau_mensualites2=zeros(1,nb_mois);  
 
// ---------------------------------------------------------  
 
exec taux_cac.sci ;  
tableau_taux=tableau_taux_cac40;  
 
getf bourse.sci  
mois_tab=01;  
annee_tab=1965;  
 
// ---------------------------------------------------------  
// ---------------------------------------------------------  
 
[capital_cac,plus_values_cac]=bourse(...  
mois_tab,annee_tab,tableau_taux,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin);  
 
[capital_cac2,plus_values_cac2]=bourse(...  
mois_tab,annee_tab,tableau_taux,capital_initial,tableau_mensualites2,...  
mois_debut,annee_debut,mois_fin,annee_fin);  
 
// ------------------------------------------------------------  
// Graphique  
// ------------------------------------------------------------  
 
 
xset('window',1); xbasc();  
 
plot2d2(mois,[capital_cac ; capital_cac2]');  
 
xtitle('Capital initial de' +...  
string(capital_initial) +' euros'+' et placements reguliers de '+...  
string(tableau_mensualites(1)) +' euros', 'Mois' ,'Capital');  
 
legends(['Bourse de  '+string(mois_debut)+'/'+string(annee_debut)+...  
 '  a  '+string(mois_fin)+'/'+string(annee_fin)+', avec mensualites',...  
 'Bourse de  '+string(mois_debut)+'/'+string(annee_debut)+...  
 '  a  '+string(mois_fin)+'/'+string(annee_fin)+', sans mensualites'],...  
 [1,2],'ul');  
 
//

PIC

Figure 6: Comparaison de capitalisations boursières selon les mensualités

Date d’entréedate de sortiemensualitécapital initial
01/1985 01/1995 100 class="td11"> 1 000
01/1985 01/1995 0 class="td11"> 1 000

Table 5: Données pour comparaison de capitaux en bourse, selon les mensualites
Comparaison d’un même placement sur deux périodes différentes

On va ici simuler un même placement, mais sur deux plages historiques différentes. Le programme associé est celui du Code Scilab 10. Une fois encore, le graphique, obtenu avec les données du Tableau 3.3, est en Figure 7.

Code Scilab 10.

//

//  -----------------------------------------------------------  
//  Données  
//  --------------------------------------------------------  
mois_debut=06;  
annee_debut=1993;  
mois_fin=06;  
annee_fin=2003;  
mois=0:((12-mois_debut) + (annee_fin - annee_debut-1)*12 +...  
mois_fin);  
nb_mois=length(mois);  
 
capital_initial=1000;  
tableau_mensualites=100*ones(1,nb_mois);  
 
//  ----------------------------------------------------------  
 
mois_debut2=01;  
annee_debut2=1975;  
mois_fin2=01;  
annee_fin2=1985;  
 
//  --------------------------------------------------------  
//  --------------------------------------------------------  
 
exec taux_cac.sci ;  
tableau_taux=tableau_taux_cac40;  
 
getf bourse.sci  
mois_tab=01;  
annee_tab=1965;  
 
[capital_cac,plus_values_cac]=bourse(...  
mois_tab,annee_tab,tableau_taux,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin);  
 
[capital_cac2,plus_values_cac2]=bourse(...  
mois_tab,annee_tab,tableau_taux,capital_initial,tableau_mensualites,...  
mois_debut2,annee_debut2,mois_fin2,annee_fin2);  
 
 
 
// ---------------------------------------------------------  
// Graphiques  
// ---------------------------------------------------------  
 
 
xset('window',1); xbasc();  
 
plot2d2(mois,[capital_cac ; capital_cac2]');  
 
xtitle('Capital initial de' +...  
string(capital_initial) +' euros'+' et placements reguliers de '+...  
string(tableau_mensualites(1)) +' euros', 'Mois' ,'Capital');  
 
legends(['Bourse de  '+string(mois_debut)+'/'+string(annee_debut)+...  
 '  a  '+string(mois_fin)+'/'+string(annee_fin),...  
'Bourse de  '+string(mois_debut2)+'/'+string(annee_debut2)+...  
 '  a  '+string(mois_fin2)+'/'+string(annee_fin2)],[1,2],'ul');  
 
//

PIC

Figure 7: Comparaison de capitalisations boursières à différentes époques

Date d’entréedate de sortiemensualitécapital initial
06/1993 06/2003 100 class="td11"> 1 000
01/1975 01/1985 100 class="td11"> 1 000

Table 6: Données pour comparaison de capitaux en bourse, selon les dates de placement

3.4 Comparaison des trois différents placements

Il s’agit ici de comparer les placements sur le livret A, l’assurance-vie ou la bourse. Les programmes associés sont donnés en Code Scilab 11

Code Scilab 11.

//

getf('annuel.sci');  
 
 
// ------------------------------------------------------------  
// Données communes  
// ------------------------------------------------------------  
 
mois_debut=01;  
annee_debut=1965;  
mois_fin=06;  
annee_fin=2002;  
mois=0:((12-mois_debut) + (annee_fin - annee_debut-1)*12 +...  
mois_fin);  
nb_mois=length(mois);  
 
capital_initial=1000;  
tableau_mensualites=100*ones(1,nb_mois);  
 
 
// ------------------------------------------------------------  
// Livret A  
// ------------------------------------------------------------  
 
taux_A=2.75;  
tableau_taux=taux_A*ones(1,nb_mois);  
 
[capital_A,total_interets_A]=annuel(...  
tableau_taux,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin)  
 
 
// ------------------------------------------------------------  
// Assurance-vie  
// ------------------------------------------------------------  
 
taux_av=4.5;  
frais=3;  
 
tableau_taux_av=taux_av*ones(1,nb_mois);  
 
getf av2.sci;  
 
 [capital_av,total_interets_av]=assurance_vie(...  
 tableau_taux_av,frais,capital_initial,tableau_mensualites,...  
mois_debut,annee_debut,mois_fin,annee_fin);  
 
// ------------------------------------------------------------  
// CAC 40  
// ------------------------------------------------------------  
 
exec taux_cac.sci ;  
tableau_taux=tableau_taux_cac40;  
 
getf bourse.sci  
 
mois_tab=01;  
annee_tab=1965;  
 
[capital_cac,plus_values_cac]=stock(...  
mois_tab,annee_tab,tableau_taux,capital_initial,...  
tableau_mensualites,mois_debut,annee_debut,mois_fin,annee_fin)  
 
 
 
// ------------------------------------------------------------  
// Graphiques  
// ------------------------------------------------------------  
 
 
xset('window',1); xbasc();  
 
plot2d2(mois,[capital_A ; capital_av ; capital_cac]')  
 
xtitle('Capital initial de' +...  
string(capital_initial) +' euros'+' et placements reguliers de '+...  
string(tableau_mensualites(1)) +' euros', 'Mois' ,'Capital');  
 
legends(['Livret A '+string(taux_A)+'%' ; ...  
 'Assurance-vie '+string(taux_av)+'%' ; 'CAC 40'],[1,2,3],'ul');  
 
//

Le graphique de synthèse est donné en Figure 3.4, et correspond aux données du Tableau 3.4

PIC

Figure 8: Graphique de synthèse : comparaison sur 10 ans

Placement taux fraisdate d’entréedate de sortiemensualitécapital initial
Assurance-vie 4,5% 3 % 01/1965 06/2002 100 class="td11"> 1 000
LivretA 2.75 % - 01/1965 06/2002 100 class="td11"> 1 000
Bourse - - 01/1965 06/2002 100 class="td11"> 1 000

Table 7: Données pour synthèse et comparaison des placements

4 Conclusion

soigner frais d’achat et de vente, et fiscalité boursière

plafond livret A

scénarios types de placements

soigner fiscalité assurance-vie et revoir code en conséquence

A Annexe : Code spécifique pour le Livret A

Le livret A se caractérise notamment par

  • l’absence de frais d’entrée ou de sortie,
  • son mécanisme de calcul des intérêts par quinzaine et de capitalisation par année,
  • son taux, fixe au moins pour de courtes périodes, et relativement faible.

A.1 Programme Scilab

Le programme présenté en Code Scilab 12 définit une fonction Scilab, appelée livretA, qui prend en arguments :

  • le taux du livret ;
  • le montant du capital initial ;
  • le montant d’un éventuel apport régulier d’argent ;
  • et les dates de placement initial et de retrait ;

et qui renvoie trois vecteurs :

  • un premier comptant les quinzaines du placement ;
  • un deuxième qui stocke, pour chaque quinzaine, le montant du capital à cette date ;
  • un dernier qui contient, pour chaque quinzaine, le montant des intérêts agrégés.

Code Scilab 12.

//

function [abcisses_quinzaines,capital,tableau_interets]=...  
  livretA(taux,capital_initial,rajout,j1,m1,a1,j2,m2,a2)  
 
//taux en pourcentage annuel : par exemple 4 et non pas 0.04  
//capital_initial:capital initial  
//rajout:rajout chaque mois  
//placement le j1/m1/a1  
//nous sommes le j2/m2/a2  
 
//   error('Attention : mettre 4.5 pour  
//   un taux de 4,5 pourcent')  
 
t=1/24*taux  
// t est le taux par quinzaine  
 
 
////////////////////////////////////////////////////  
// PASSAGE DE DATES À DES QUINZAINES  
////////////////////////////////////////////////////  
 
if j1>15 then  
quinzaine_placement=2*m1;  
else quinzaine_placement=2*m1-1;  
end  
 
if j2>15 then  
quinzaine_sortie=2*m2-1;  
else quinzaine_sortie=2*(m2-1);  
end  
//Commentaire : quinzaine_sortie idem que  
//quinzaines_restantes mais pour le retrait  
 
 
////////////////////////////////////////////////////  
//  
////////////////////////////////////////////////////  
 
nombre_annees=a2-a1-1;  
 
// initialisation  
 
////////////////////////////////////////////////////  
// PREMIÈRE ANNÉE  
////////////////////////////////////////////////////  
 
quinzaines_restantes=24-quinzaine_placement;  
 
abcisses_quinzaines= ...  
1:(quinzaines_restantes+quinzaine_sortie+nombre_annees*24+1);  
// vecteur des abscisses exprimées en quinzaines  
 
 
// Commentaire:  
// quinzaines_restantes est le nombre de quinzaines  
//de l'année du placement pendant lesquelles  
//l'argent est placé  
 
// Problème car les versements sont mensuels alors que  
//le calcul des intérêts est par quinzaines  
 
// capital est un vecteur contenant la suite des capitaux  
//par quinzaine  
// interets est un scalaire  
 
capital=[]  
tableau_interets=[];  
interets=0;  
 
if j1>15 then  
  // alors quinzaines_restantes est pair  
  capital=capital_initial;  
  tableau_interets=[0];  
        for j=1:(quinzaines_restantes/2)  
  // boucle sur le mois  
  capital=[capital,capital($)+rajout,capital($)+rajout]  
  // doublon pour cause de quinzaines  
  interets=interets+2*t/100*capital($);  
  tableau_interets=[tableau_interets,tableau_interets($)+...  
  t/100*capital($),tableau_interets($)+2*t/100*capital($)];  
  // cumul des intérêts  
        end  
 
else  
   // j1<=15 et alors quinzaines_restantes est impair  
   capital=[capital_initial,capital_initial + 0]  
   interets=t/100*capital($);  
 tableau_interets=[0,t/100*capital($)];  
// +0 pour signifier l'absence de rajout dans  
//la deuxième quinzaine  
for j=1:(quinzaines_restantes-1)/2  
  // boucle sur le mois  
  capital=[capital,capital($)+rajout,capital($)+rajout]  
  // doublon pour cause de quinzaines  
  interets=interets+2*t/100*capital($);  
  tableau_interets=[tableau_interets,tableau_interets($)+...  
  t/100*capital($),tableau_interets($)+2*t/100*capital($)];  
  // cumul des intérêts  
end  
end  
 
capital($)=capital($)+interets ;  
// capital à la fin de la première année  
 
 
////////////////////////////////////////////////////  
// ANNÉES INTERMÉDIAIRES  
////////////////////////////////////////////////////  
 
 
if nombre_annees >0 then  
   for i=1:nombre_annees  
        interets=0;  
        for j=1:12  
  capital=[capital,capital($)+rajout,capital($)+rajout]  
  interets=interets+2*t/100*capital($);  
  tableau_interets=[tableau_interets,tableau_interets($)+...  
  t/100*capital($), tableau_interets($)+2*t/100*capital($)];  
        end  
capital($)=capital($)+interets ;  
// capital à la fin de chaque année  
   end  
end  
 
 
////////////////////////////////////////////////////  
// DERNIÈRE ANNÉE  
////////////////////////////////////////////////////  
 
interets=0;  
 
if j2>15 then  
        for j=1:((quinzaine_sortie-1)/2)  
  capital=[capital,capital($)+rajout,capital($)+rajout]  
  interets=interets+2*t/100*capital($);  
  tableau_interets=[tableau_interets,tableau_interets($)+...  
  t/100*capital($), tableau_interets($)+2*t/100*capital($)];  
        end  
capital=[capital,capital($)+rajout]  
interets=interets+t/100*capital($);  
tableau_interets=[tableau_interets,tableau_interets($)+t/100*capital($)];  
else  
        for j=1:quinzaine_sortie/2  
  capital=[capital,capital($)+rajout,capital($)+rajout]  
  interets=interets+2*t/100*capital($);  
  tableau_interets=[tableau_interets,tableau_interets($)+...  
  t/100*capital($), tableau_interets($)+2*t/100*capital($)];  
        end  
end  
 
capital($)=capital($)+interets;  
 
CAPITAL=capital($);  
 
printf('Le capital en sortie est :')  
disp(CAPITAL);  
endfunction  
 
 
 
// 

A.2 Exemple

Un exemple d’utilisation de la fonction livretA est donné en Code Scilab 13. Ceci signifie que

  • le taux du livret A est 2,75 % ;
  • le montant du capital initial est de 1 000 euros ;
  • le montant de l’apport régulier d’argent est de 100 euros mensuels ;
  • et 10/05/2007 et 27/10/2017 sont les dates de placement initial et de retrait.

Le graphique correspondant est donné en Figure 9.

Code Scilab 13.

//

taux=2.75;  
capital_initial=1000;  
rajout=100;  
j1=10;  
m1=05;  
a1=2007;  
j2=27;  
m2=10;  
a2=2017;  
 
getf('livretA.sci');  
 
[abscisses_quinzaines,capital,tableau_interets]=...  
  livretA(taux,capital_initial,rajout,j1,m1,a1,j2,m2,a2);  
 
 xbasc();  
plot2d2(abscisses_quinzaines,capital);  
 
xtitle('Capital initial ' +string(capital_initial) +...  
' euros'+' et placements reguliers de '+string(rajout) +' euros',...  
   'Quinzaines' ,'Capital');  
 
legends(['Livret A '+string(taux)+'%'],[1],'ul');  
 
// 

PIC

Figure 9: Placement sur livret A. Évolution du capital pour les données relatives au Tableau A.2.

Tauxdate d’entréedate de sortiemensualitécapital initial
2,75% 10/05/2007 27/10/2017 100 class="td11"> 1 000

Table 8: Données pour simulation de placement régulier sur le livret A
L'École des Ponts ParisTech est membre fondateur de

L'École des Ponts ParisTech est certifiée 
ParisTech ParisEst ParisTech

 

Offres d’emploi - Appel d'offres et publications légales - Charte graphique - Mentions légales - Accessibilité - Plan du site - Venir à l’école - Nous contacter
Rejoignez-nous sur :           
Copyright 2014
École des Ponts ParisTech
All rights reserved